3. Algorithms

The algorithms module is intended to contain some specific algorithms in order to execute very common evolutionary algorithms. The method used here are more for convenience than reference as the implementation of every evolutionary algorithm may vary infinitly. Most of the algorithms in this module use operators registered in the toolbox with the same keywords, mate() for crossover, mutate() for mutation, select() for selection and evaluate() for evaluation.

You are encouraged to write your own algorithms in order to make them do what you realy want them to do.

eap.algorithms.eaSimple(toolbox, population, cxpb, mutpb, ngen[, halloffame])

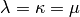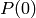This algorithm reproduce the simplest evolutionary algorithm as presented in chapter 7 of Back, Fogel and Michalewicz, “Evolutionary Computation 1 : Basic Algorithms and Operators”, 2000. It uses and goes as follow. It first initializes the population () by evaluating every individual presenting an invalid fitness. Then, it enters the evolution loop that begins by the selection of the 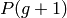population. Then the crossover operator is applied on a proportion of 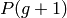according to the cxpb probability, the resulting and the untouched individuals are placed in 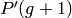. Thereafter, a proportion of 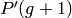, determined by mutpb, is mutated and placed in 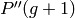, the untouched individuals are transfered 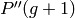. Finally, those new individuals are evaluated and the evolution loop continues until ngen generations are completed. Briefly, the operators are applied in the following order

evaluate(population)
for i in range(ngen):
    offsprings = select(population)
    offsprings = mate(offsprings)
    offsprings = mutate(offsprings)
    evaluate(offsprings)
    population = offsprings

eap.algorithms.eaMuPlusLambda(toolbox, population, mu, lambda_, cxpb, mutpb, ngen[, halloffame])

This is the 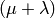evolutionary algorithm. First, the individuals having an invalid fitness are evaluated. Then, the evolutionary loop begins by producing lambda offsprings from the population, the offsprings are generated by a crossover, a mutation or a reproduction proportionally to the probabilities cxpb, mutpb and 1 - (cxpb + mutpb). The offsprings are then evaluated and the next generation population is selected from both the offsprings and the population. Briefly, the operators are applied as following

evaluate(population)
for i in range(ngen):
    offsprings = generate_offsprings(population)
    evaluate(offsprings)
    population = select(population + offsprings)

Note

Both produced individuals from the crossover are put in the offspring pool.

eap.algorithms.eaMuCommaLambda(toolbox, population, mu, lambda_, cxpb, mutpb, ngen[, halloffame])

This is the 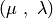evolutionary algorithm. First, the individuals having an invalid fitness are evaluated. Then, the evolutionary loop begins by producing lambda offsprings from the population, the offsprings are generated by a crossover, a mutation or a reproduction proportionally to the probabilities cxpb, mutpb and 1 - (cxpb + mutpb). The offsprings are then evaluated and the next generation population is selected only from the offsprings. Briefly, the operators are applied as following

evaluate(population)
for i in range(ngen):
    offsprings = generate_offsprings(population)
    evaluate(offsprings)
    population = select(offsprings)

Note

Both produced individuals from the crossover are put in the offspring pool.

eap.algorithms.eaSteadyState(toolbox, population, ngen[, halloffame])

The is the steady-state evolutionary algorithm