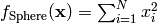7. Benckmarks¶

Regroup typical EC benchmarks functions to import easily and benchmark examples.

deap.benchmarks.ackley(individual)¶

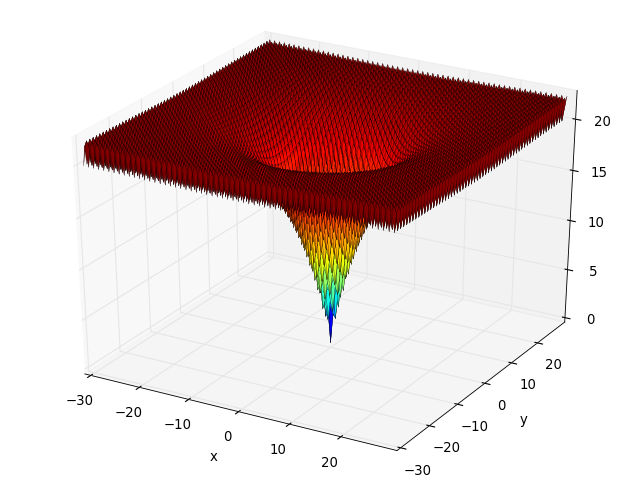
Ackley test objective function.

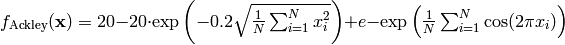
$f_{\text{Ackley}}(\mathbf{x}) = 20 - 20\cdot\exp\left(-0.2\sqrt{\frac{1}{N} \sum_{i=1}^N x_i^2} \right) + e - \exp\left(\frac{1}{N}\sum_{i=1}^N \cos(2\pi x_i) \right)$

(Source code, png, hires.png, pdf)

deap.benchmarks.bohachevsky(individual)¶

Bohachevsky test objective function

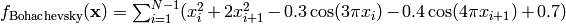
$f_{\text{Bohachevsky}}(\mathbf{x}) = \sum_{i=1}^{N-1}(x_i^2 + 2x_{i+1}^2 - 0.3\cos(3\pi x_i) - 0.4\cos(4\pi x_{i+1}) + 0.7)$

(Source code, png, hires.png, pdf)

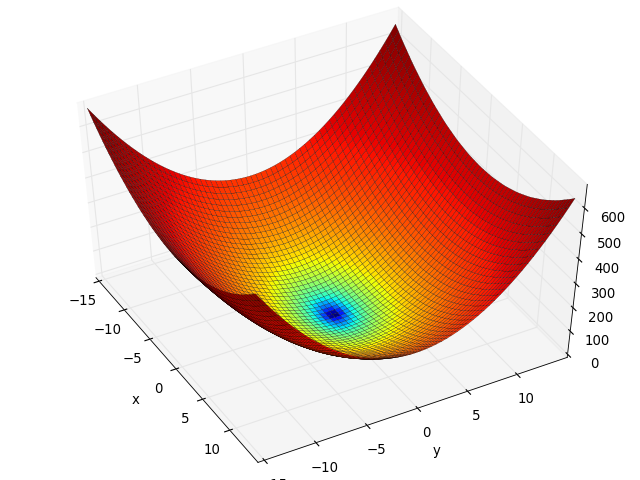
deap.benchmarks.cigar(individual)¶

Cigar test objective function.

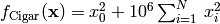
$f_{\text{Cigar}}(\mathbf{x}) = x_0^2 + 10^6\sum_{i=1}^N\,x_i^2$

deap.benchmarks.griewank(individual)¶

Griewank test objective function

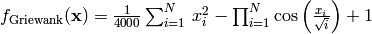
$f_{\text{Griewank}}(\mathbf{x}) = \frac{1}{4000}\sum_{i=1}^N\,x_i^2 - \prod_{i=1}^N\cos\left(\frac{x_i}{\sqrt{i}}\right) + 1$

(Source code, png, hires.png, pdf)

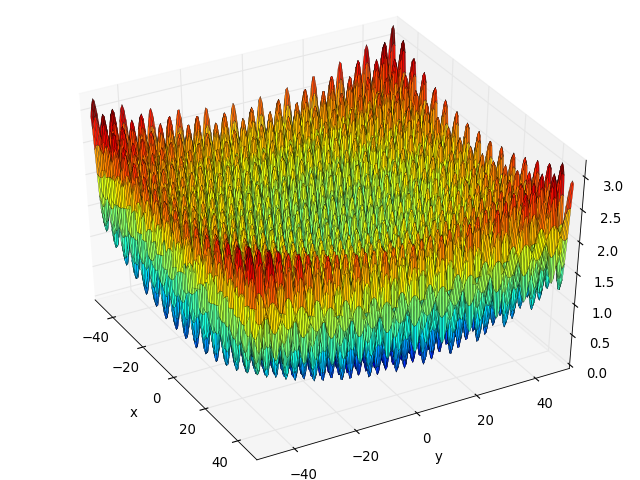
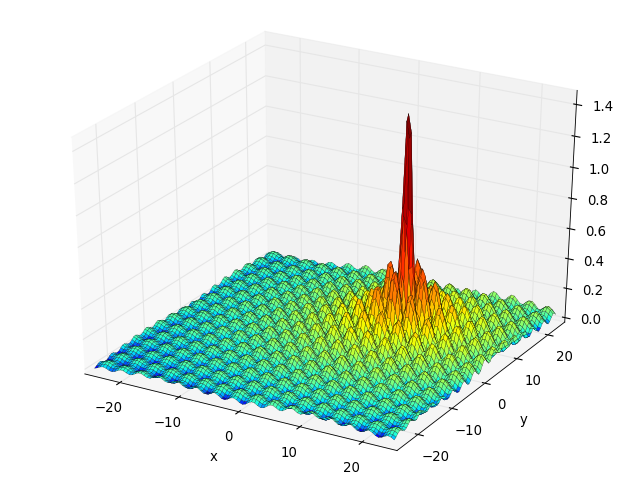
deap.benchmarks.h1(individual)¶

Simple two-dimensional function containing several local maxima, H1 has a unique maximum value of 2.0 at the point (8.6998, 6.7665). From : The Merits of a Parallel Genetic Algorithm in Solving Hard Optimization Problems, A. J. Knoek van Soest and L. J. R. Richard Casius, J. Biomech. Eng. 125, 141 (2003)

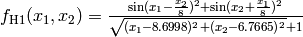
$f_{\text{H1}}(x_1, x_2) = \frac{\sin(x_1 - \frac{x_2}{8})^2 + \sin(x_2 + \frac{x_1}{8})^2}{\sqrt{(x_1 - 8.6998)^2 + (x_2 - 6.7665)^2} + 1}$

(Source code, png, hires.png, pdf)

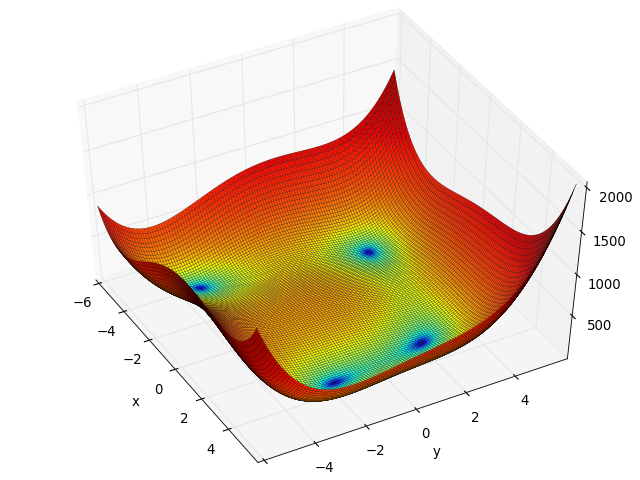
deap.benchmarks.himmelblau(individual)¶

The Himmelblau’s function is multimodal with 4 defined minimums in $[-6, 6]^2$ .

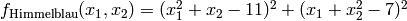
$f_{\text{Himmelblau}}(x_1, x_2) = (x_1^2 + x_2 - 11)^2 + (x_1 + x_2^2 -7)^2$

(Source code, png, hires.png, pdf)

deap.benchmarks.kursawe(individual)¶

Kursawe multiobjective function.

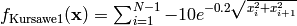
$f_{\text{Kursawe}1}(\mathbf{x}) = \sum_{i=1}^{N-1} -10 e^{-0.2 \sqrt{x_i^2 + x_{i+1}^2} }$

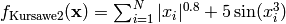
$f_{\text{Kursawe}2}(\mathbf{x}) = \sum_{i=1}^{N} |x_i|^{0.8} + 5 \sin(x_i^3)$

(Source code, png, hires.png, pdf)

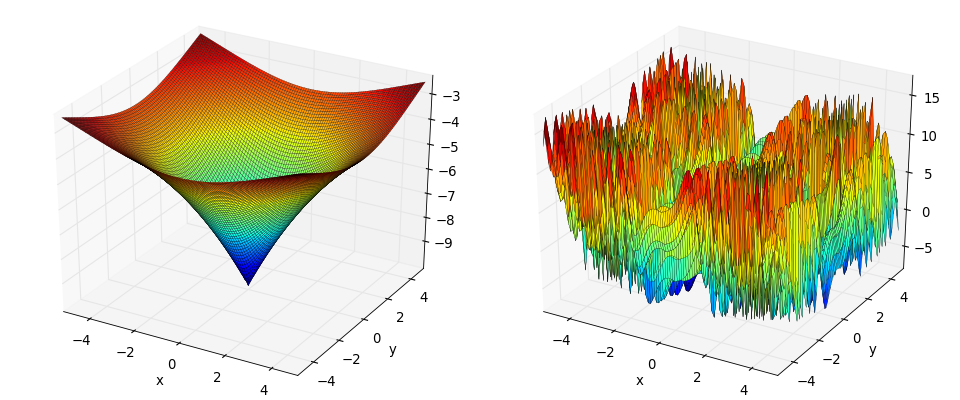
deap.benchmarks.plane(individual)¶

Plane test objective function.

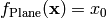
$f_{\text{Plane}}(\mathbf{x}) = x_0$

deap.benchmarks.rand(individual)¶

Random test objective function.

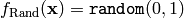
$f_{\text{Rand}}(\mathbf{x}) = \text{\texttt{random}}(0,1)$

deap.benchmarks.rastrigin(individual)¶

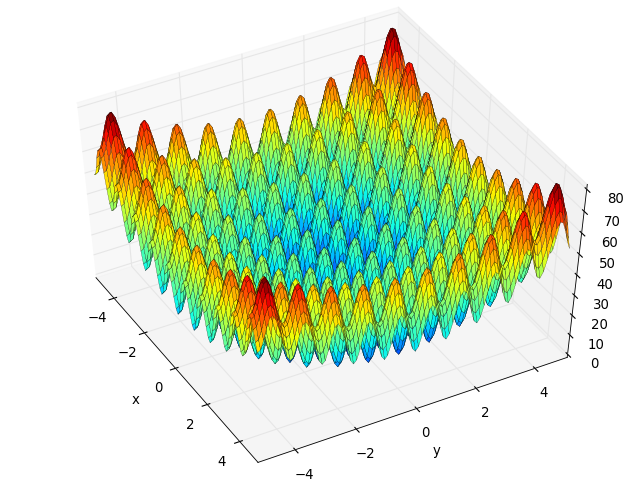
Rastrigin test objective function.

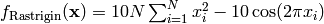
$f_{\text{Rastrigin}}(\mathbf{x}) = 10N \sum_{i=1}^N x_i^2 - 10 \cos(2\pi x_i)$

(Source code, png, hires.png, pdf)

deap.benchmarks.rastrigin_scaled(individual)¶

Scaled Rastrigin test objective function

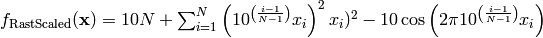
$f_{\text{RastScaled}}(\mathbf{x}) = 10N + \sum_{i=1}^N \left(10^{\left(\frac{i-1}{N-1}\right)} x_i \right)^2 x_i)^2 - 10\cos\left(2\pi 10^{\left(\frac{i-1}{N-1}\right)} x_i \right)$

deap.benchmarks.rastrigin_skew(individual)¶

Skewed Rastrigin test objective function

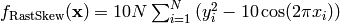
$f_{\text{RastSkew}}(\mathbf{x}) = 10N \sum_{i=1}^N \left(y_i^2 - 10 \cos(2\pi x_i)\right)$

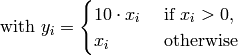
$\text{with } y_i = \begin{cases} 10\cdot x_i & \text{ if } x_i > 0,\\ x_i & \text{ otherwise } \end{cases}$

deap.benchmarks.rosenbrock(individual)¶

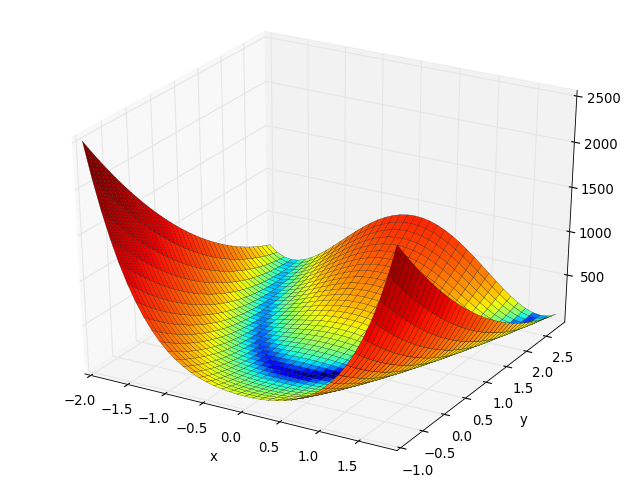
Rosenbrock test objective function.

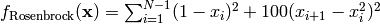
$f_{\text{Rosenbrock}}(\mathbf{x}) = \sum_{i=1}^{N-1} (1-x_i)^2 + 100 (x_{i+1} - x_i^2 )^2$

(Source code, png, hires.png, pdf)

deap.benchmarks.schaffer(individual)¶

Schaffer test objective function.

$f_{\text{Schaffer}}(\mathbf{x}) = \sum_{i=1}^{N-1} (x_i^2+x_{i+1}^2)^{0.25} \cdot \left[ \sin^2(50\cdot(x_i^2+x_{i+1}^2)^{0.10}) + 1.0 \right]$

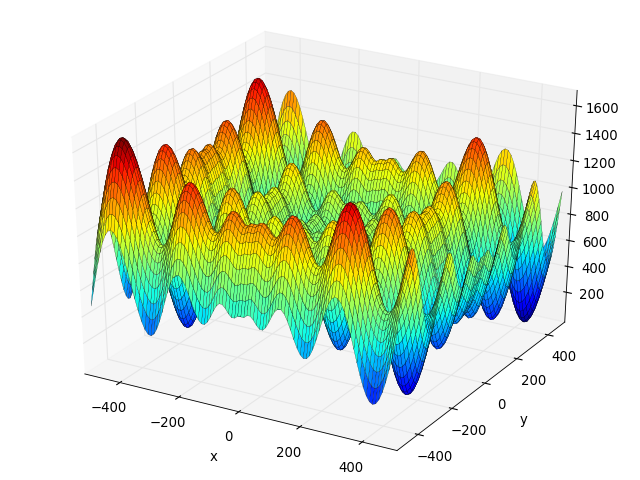
deap.benchmarks.schwefel(individual)¶

Schwefel test objective function.

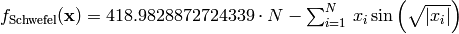
$f_{\text{Schwefel}}(\mathbf{x}) = 418.9828872724339\cdot N - \sum_{i=1}^N\,x_i\sin\left(\sqrt{|x_i|}\right)$

(Source code, png, hires.png, pdf)

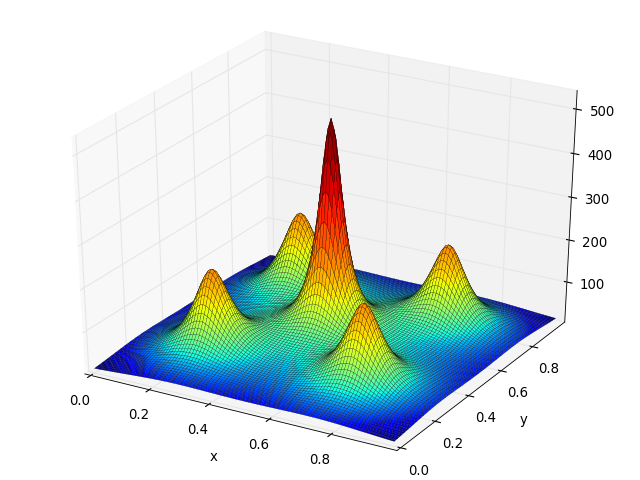
deap.benchmarks.shekel(individual, a, c)¶

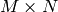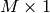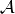The Shekel multimodal function can have any number of maxima. The number of maxima is given by the length of any of the arguments a or c, a is a matrix of size $M\times N$ , where M is the number of maxima and N the number of dimensions and c is a $M\times 1$ vector. The matrix $\mathcal{A}$ can be seen as the position of the maxima and the vector $\mathbf{c}$ , the width of the maxima.

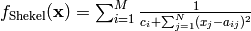
$f_\text{Shekel}(\mathbf{x}) = \sum_{i = 1}^{M} \frac{1}{c_{i} + \sum_{j = 1}^{N} (x_{j} - a_{ij})^2 }$

The following figure uses

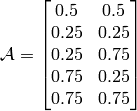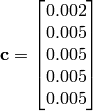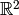$\mathcal{A} = \begin{bmatrix} 0.5 & 0.5 \\ 0.25 & 0.25 \\ 0.25 & 0.75 \\ 0.75 & 0.25 \\ 0.75 & 0.75 \end{bmatrix}$ and $\mathbf{c} = \begin{bmatrix} 0.002 \\ 0.005 \\ 0.005 \\ 0.005 \\ 0.005 \end{bmatrix}$ , thus defining 5 maximums in $\mathbb{R}^2$ .