9. A Pi Calculation with DTM

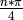A simple yet interesting use of DTM is the calculation of with a Monte Carlo approach. This approach is quite straightforward : if you randomly throw n darts on a unit square, approximately will be inside a quadrant delimited by (0,1) and (1,0). Therefore, if a huge quantity of darts are thrown, one could estimate simply by computing the ratio between the number of darts inside and outside the quadrant. A comprehensive explanation of the algorithm can be found here

Note

This example is intended to show a simple parallelization of an actual algorithm. It should not be taken as a good calculation algorithm (it is not).

A possible serial Python code reads as follow :

from random import random
from math import hypot

def test(tries):
    # Each run of this function makes some tries
    # and return the number of darts inside the quadrant (r < 1)
    return sum(hypot(random(), random()) < 1 for i in xrange(tries))

def calcPi(n, t):
    expr = (test(t) for i in range(n))
    pi2 = 4. * sum(expr) / (n*t)
    print("pi = " + str(pi2))
    return pi2

piVal = calcPi(1000, 10000)

With DTM, you can now take advantage of the parallelization, and distribute the calls to the function test(). There are many ways to do so, but a mere one is to use repeat(), which repeats a function an arbitrary number of times, and returns a results list. In this case, the program may look like this :

from math import hypot
from random import random
from deap import dtm

def test(tries):
    # Each run of this function makes some tries
    # and return the number of darts inside the quadrant (r < 1)
    return sum(hypot(random(), random()) < 1 for i in xrange(tries))

def calcPi(n, t):
    expr = dtm.repeat(test, n, t)
    pi2 = 4. * sum(expr) / (n*t)
    print("pi = " + str(pi2))
    return pi2

piVal = dtm.start(calcPi, 1000, 10000)

And so, without any major changes (and not at all in the test() function), this computation can be distributed.