5. GP Even-Parity problem

Parity is one of the classical GP problems. The goal is to find a program that produces the value of the Boolean even parity given n independent Boolean inputs. Usually, 6 Boolean inputs are used (Parity-6), and the goal is to match the good parity bit value for each of the 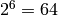possible entries. The problem can be made harder by increasing the number of inputs (in the DEAP implementation, this number can easily be tuned, as it is fixed by a constant named PARITY_FANIN_M).

For more information about this problem, see Reference.

5.1. Primitives set used

Parity uses standard Boolean operators as primitives, available in the Python operator module :

pset = gp.PrimitiveSet("MAIN", PARITY_FANIN_M, "IN")
pset.addPrimitive(operator.and_, 2)
pset.addPrimitive(operator.or_, 2)
pset.addPrimitive(operator.xor, 2)
pset.addPrimitive(operator.not_, 1)
pset.addTerminal(1)
pset.addTerminal(0)

In addition to the n inputs, we add two constant terminals, one at 0, one at 1.

Note

As Python is a dynamic typed language, you can mix Boolean operators and integers without any issue.

5.2. Evaluation function

In this implementation, the fitness of a Parity individual is simply the number of successful cases. Thus, the fitness is maximized, and the maximum value is 64 in the case of a 6 inputs problems.

def evalParity(individual):
    func = toolbox.lambdify(expr=individual)
    good = sum(func(*inputs[i]) == outputs[i] for i in xrange(PARITY_SIZE_M))
    return good,

inputs and outputs are two pre-generated lists, to speedup the evaluation, mapping a given input vector to the good output bit. The Python sum() function works on booleans (false is interpreted as 0 and true as 1), so the evaluation function boils down to sum the number of successful tests : the higher this sum, the better the individual.

5.3. Complete example

The other parts of the program are greatly the same as the Symbolic Regression algorithm :

from deap import algorithms
from deap import base
from deap import creator
from deap import tools
from deap import gp


logging.basicConfig(level=logging.DEBUG, stream=sys.stdout)

# Initialize Parity problem input and output matrices
PARITY_FANIN_M = 6
PARITY_SIZE_M = 2**PARITY_FANIN_M

inputs = [None] * PARITY_SIZE_M
outputs = [None] * PARITY_SIZE_M

for i in xrange(PARITY_SIZE_M):
    inputs[i] = [None] * PARITY_FANIN_M
    value = i
    dividor = PARITY_SIZE_M
    parity = 1
    for j in xrange(PARITY_FANIN_M):
        dividor /= 2
        if value >= dividor:
            inputs[i][j] = 1
            parity = int(not parity)
            value -= dividor
        else:
            inputs[i][j] = 0
    outputs[i] = parity

pset = gp.PrimitiveSet("MAIN", PARITY_FANIN_M, "IN")
pset.addPrimitive(operator.and_, 2)
pset.addPrimitive(operator.or_, 2)
pset.addPrimitive(operator.xor, 2)
pset.addPrimitive(operator.not_, 1)
pset.addTerminal(1)
pset.addTerminal(0)

creator.create("FitnessMax", base.Fitness, weights=(1.0,))
creator.create("Individual", gp.PrimitiveTree, fitness=creator.FitnessMax, pset=pset)

toolbox = base.Toolbox()
toolbox.register("expr", gp.genFull, pset=pset, min_=3, max_=5)
toolbox.register("individual", tools.initIterate, creator.Individual, toolbox.expr)
toolbox.register("population", tools.initRepeat, list, toolbox.individual)
toolbox.register("lambdify", gp.lambdify, pset=pset)

def evalParity(individual):
    func = toolbox.lambdify(expr=individual)
    good = sum(func(*inputs[i]) == outputs[i] for i in xrange(PARITY_SIZE_M))
    return good,

toolbox.register("evaluate", evalParity)
toolbox.register("select", tools.selTournament, tournsize=3)
toolbox.register("mate", gp.cxUniformOnePoint)
toolbox.register("expr_mut", gp.genGrow, min_=0, max_=2)
toolbox.register("mutate", gp.mutUniform, expr=toolbox.expr_mut)

def main():
    random.seed(21)
    pop = toolbox.population(n=300)
    hof = tools.HallOfFame(1)
    stats = tools.Statistics(lambda ind: ind.fitness.values)
    stats.register("Avg", tools.mean)
    stats.register("Std", tools.std)
    stats.register("Min", min)
    stats.register("Max", max)
    
    algorithms.eaSimple(toolbox, pop, 0.5, 0.2, 40, stats, halloffame=hof)
    
    logging.info("Best individual is %s, %s", gp.evaluate(hof[0]), hof[0].fitness)
    
    return pop, stats, hof

if __name__ == "__main__":
    main()

Note

The import of the Python standard library modules are not shown.

5.4. Reference

John R. Koza, “Genetic Programming II: Automatic Discovery of Reusable Programs”, MIT Press, 1994, pages 157-199.