7. Benchmarks¶

Regroup typical EC benchmarks functions to import easily and benchmark examples.

Single Objective Continuous	Multi Objective Continuous	Binary
`cigar()`	`fonseca()`	`chuang_f1()`
`plane()`	`kursawe()`	`chuang_f2()`
`sphere()`	`schaffer_mo()`	`chuang_f3()`
`ackley()`	`dtlz1()`	`royal_road1()`
`bohachevsky()`	`dtlz2()`	`royal_road2()`
`griewank()`	`dtlz3()`
`h1()`	`dtlz4()`
`himmelblau()`	`zdt1()`
`rastrigin()`	`zdt2()`
`rastrigin_scaled()`	`zdt3()`
`rastrigin_skew()`	`zdt4()`
`rosenbrock()`	`zdt6()`
`schaffer()`
`schwefel()`
`shekel()`

7.1. Continuous Optimization¶

deap.benchmarks.cigar(individual)¶

Cigar test objective function.

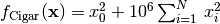
$f_{\text{Cigar}}(\mathbf{x}) = x_0^2 + 10^6\sum_{i=1}^N\,x_i^2$

deap.benchmarks.plane(individual)¶

Plane test objective function.

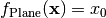
$f_{\text{Plane}}(\mathbf{x}) = x_0$

deap.benchmarks.sphere(individual)¶

Sphere test objective function.

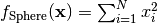
$f_{\text{Sphere}}(\mathbf{x}) = \sum_{i=1}^Nx_i^2$

deap.benchmarks.ackley(individual)¶

Ackley test objective function.

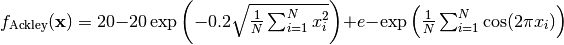
$f_{\text{Ackley}}(\mathbf{x}) = 20 - 20\exp\left(-0.2\sqrt{\frac{1}{N} \sum_{i=1}^N x_i^2} \right) + e - \exp\left(\frac{1}{N}\sum_{i=1}^N \cos(2\pi x_i) \right)$

(Source code, png, hires.png, pdf)

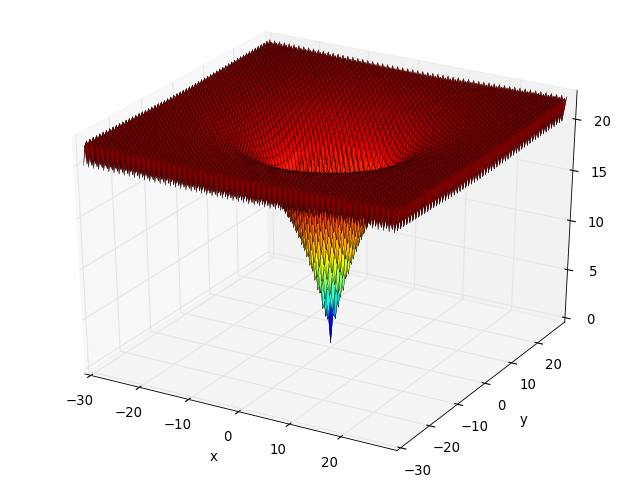
deap.benchmarks.bohachevsky(individual)¶

Bohachevsky test objective function

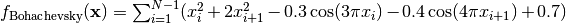
$f_{\text{Bohachevsky}}(\mathbf{x}) = \sum_{i=1}^{N-1}(x_i^2 + 2x_{i+1}^2 - 0.3\cos(3\pi x_i) - 0.4\cos(4\pi x_{i+1}) + 0.7)$

(Source code, png, hires.png, pdf)

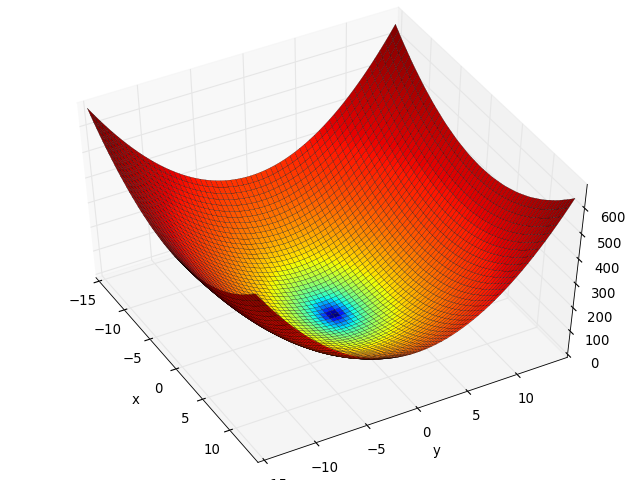
deap.benchmarks.griewank(individual)¶

Griewank test objective function

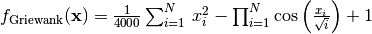
$f_{\text{Griewank}}(\mathbf{x}) = \frac{1}{4000}\sum_{i=1}^N\,x_i^2 - \prod_{i=1}^N\cos\left(\frac{x_i}{\sqrt{i}}\right) + 1$

(Source code, png, hires.png, pdf)

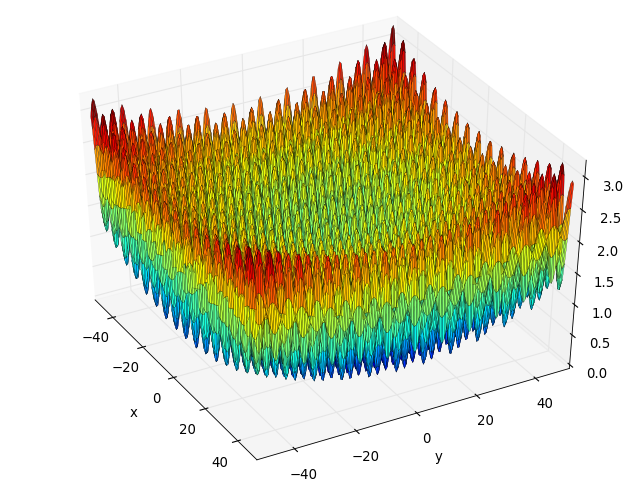
deap.benchmarks.h1(individual)¶

Simple two-dimensional function containing several local maxima, H1 has a unique maximum value of 2.0 at the point (8.6998, 6.7665). From: The Merits of a Parallel Genetic Algorithm in Solving Hard Optimization Problems, A. J. Knoek van Soest and L. J. R. Richard Casius, J. Biomech. Eng. 125, 141 (2003)

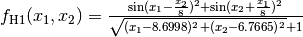
$f_{\text{H1}}(x_1, x_2) = \frac{\sin(x_1 - \frac{x_2}{8})^2 + \sin(x_2 + \frac{x_1}{8})^2}{\sqrt{(x_1 - 8.6998)^2 + (x_2 - 6.7665)^2} + 1}$

(Source code, png, hires.png, pdf)

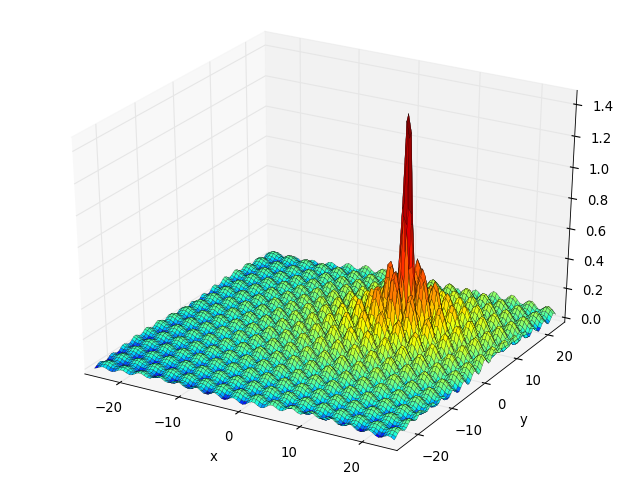
deap.benchmarks.himmelblau(individual)¶

The Himmelblau’s function is multimodal with 4 defined minimums in $[-6, 6]^2$ .

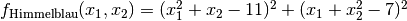
$f_{\text{Himmelblau}}(x_1, x_2) = (x_1^2 + x_2 - 11)^2 + (x_1 + x_2^2 -7)^2$

(Source code, png, hires.png, pdf)

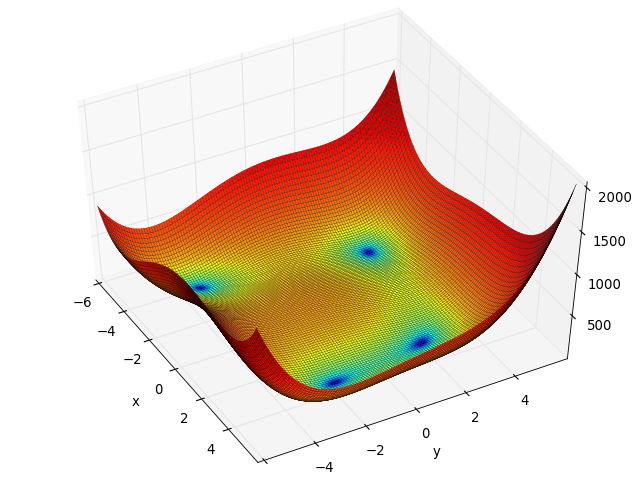
deap.benchmarks.rastrigin(individual)¶

Rastrigin test objective function.

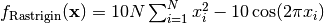
$f_{\text{Rastrigin}}(\mathbf{x}) = 10N \sum_{i=1}^N x_i^2 - 10 \cos(2\pi x_i)$

(Source code, png, hires.png, pdf)

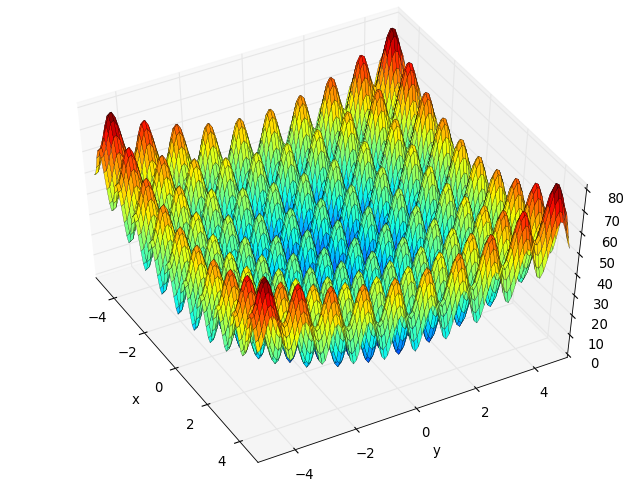
deap.benchmarks.rastrigin_scaled(individual)¶

Scaled Rastrigin test objective function,

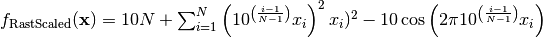
$f_{\text{RastScaled}}(\mathbf{x}) = 10N + \sum_{i=1}^N \left(10^{\left(\frac{i-1}{N-1}\right)} x_i \right)^2 x_i)^2 - 10\cos\left(2\pi 10^{\left(\frac{i-1}{N-1}\right)} x_i \right)$

deap.benchmarks.rastrigin_skew(individual)¶

Skewed Rastrigin test objective function

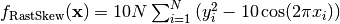
$f_{\text{RastSkew}}(\mathbf{x}) = 10N \sum_{i=1}^N \left(y_i^2 - 10 \cos(2\pi x_i)\right)$

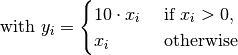
$\text{with } y_i = \begin{cases} 10\cdot x_i & \text{ if } x_i > 0,\\ x_i & \text{ otherwise } \end{cases}$

deap.benchmarks.rosenbrock(individual)¶

Rosenbrock test objective function.

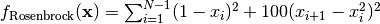
$f_{\text{Rosenbrock}}(\mathbf{x}) = \sum_{i=1}^{N-1} (1-x_i)^2 + 100 (x_{i+1} - x_i^2 )^2$

(Source code, png, hires.png, pdf)

deap.benchmarks.schaffer(individual)¶

Schaffer test objective function.

$f_{\text{Schaffer}}(\mathbf{x}) = \sum_{i=1}^{N-1} (x_i^2+x_{i+1}^2)^{0.25} \cdot \left[ \sin^2(50\cdot(x_i^2+x_{i+1}^2)^{0.10}) + 1.0 \right]$

(Source code, png, hires.png, pdf)

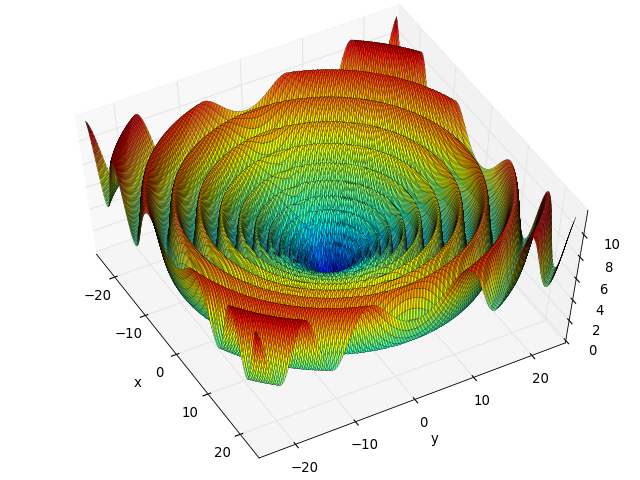
deap.benchmarks.schwefel(individual)¶

Schwefel test objective function.

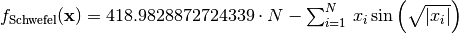
$f_{\text{Schwefel}}(\mathbf{x}) = 418.9828872724339\cdot N - \sum_{i=1}^N\,x_i\sin\left(\sqrt{|x_i|}\right)$

(Source code, png, hires.png, pdf)

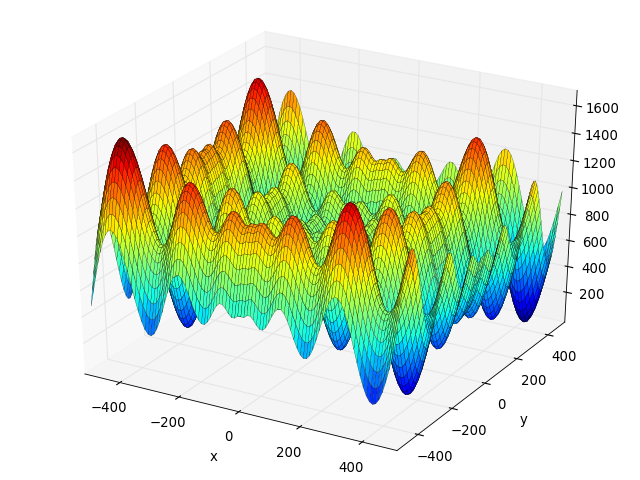
deap.benchmarks.shekel(individual, a, c)¶

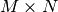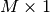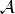The Shekel multimodal function can have any number of maxima. The number of maxima is given by the length of any of the arguments a or c, a is a matrix of size $M\times N$ , where M is the number of maxima and N the number of dimensions and c is a $M\times 1$ vector. The matrix $\mathcal{A}$ can be seen as the position of the maxima and the vector $\mathbf{c}$ , the width of the maxima.

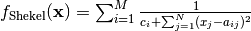
$f_\text{Shekel}(\mathbf{x}) = \sum_{i = 1}^{M} \frac{1}{c_{i} + \sum_{j = 1}^{N} (x_{j} - a_{ij})^2 }$

The following figure uses

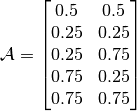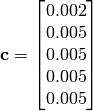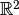$\mathcal{A} = \begin{bmatrix} 0.5 & 0.5 \\ 0.25 & 0.25 \\ 0.25 & 0.75 \\ 0.75 & 0.25 \\ 0.75 & 0.75 \end{bmatrix}$ and $\mathbf{c} = \begin{bmatrix} 0.002 \\ 0.005 \\ 0.005 \\ 0.005 \\ 0.005 \end{bmatrix}$ , thus defining 5 maximums in $\mathbb{R}^2$ .

(Source code, png, hires.png, pdf)

7.1.1. Multi-objective¶

deap.benchmarks.fonseca(individual)¶

Fonseca and Fleming’s multiobjective function. From: C. M. Fonseca and P. J. Fleming, “Multiobjective optimization and multiple constraint handling with evolutionary algorithms – Part II: Application example”, IEEE Transactions on Systems, Man and Cybernetics, 1998.

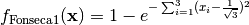
$f_{\text{Fonseca}1}(\mathbf{x}) = 1 - e^{-\sum_{i=1}^{3}(x_i - \frac{1}{\sqrt{3}})^2}$

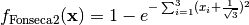
$f_{\text{Fonseca}2}(\mathbf{x}) = 1 - e^{-\sum_{i=1}^{3}(x_i + \frac{1}{\sqrt{3}})^2}$

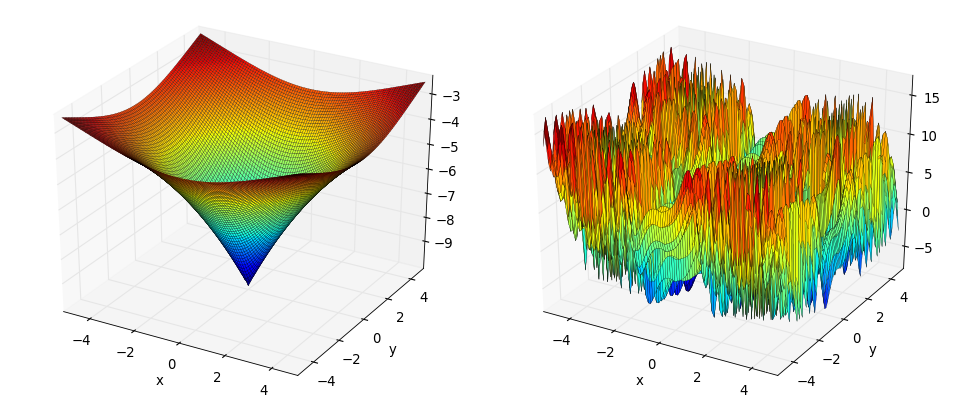
deap.benchmarks.kursawe(individual)¶

Kursawe multiobjective function.

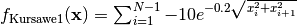
$f_{\text{Kursawe}1}(\mathbf{x}) = \sum_{i=1}^{N-1} -10 e^{-0.2 \sqrt{x_i^2 + x_{i+1}^2} }$

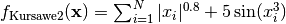
$f_{\text{Kursawe}2}(\mathbf{x}) = \sum_{i=1}^{N} |x_i|^{0.8} + 5 \sin(x_i^3)$

(Source code, png, hires.png, pdf)

deap.benchmarks.schaffer_mo(individual)¶

Schaffer’s multiobjective function on a one attribute individual. From: J. D. Schaffer, “Multiple objective optimization with vector evaluated genetic algorithms”, in Proceedings of the First International Conference on Genetic Algorithms, 1987.

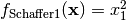
$f_{\text{Schaffer}1}(\mathbf{x}) = x_1^2$

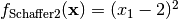
$f_{\text{Schaffer}2}(\mathbf{x}) = (x_1-2)^2$

deap.benchmarks.dtlz1(individual, obj)¶

DTLZ1 mutliobjective function. It returns a tuple of obj values. The individual must have at least obj elements. From: K. Deb, L. Thiele, M. Laumanns and E. Zitzler. Scalable Multi-Objective Optimization Test Problems. CEC 2002, p. 825 - 830, IEEE Press, 2002.

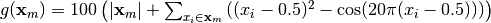
$g(\mathbf{x}_m) = 100\left(|\mathbf{x}_m| + \sum_{x_i \in \mathbf{x}_m}\left((x_i - 0.5)^2 - \cos(20\pi(x_i - 0.5))\right)\right)$

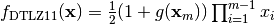
$f_{\text{DTLZ1}1}(\mathbf{x}) = \frac{1}{2} (1 + g(\mathbf{x}_m)) \prod_{i=1}^{m-1}x_i$

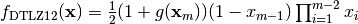
$f_{\text{DTLZ1}2}(\mathbf{x}) = \frac{1}{2} (1 + g(\mathbf{x}_m)) (1-x_{m-1}) \prod_{i=1}^{m-2}x_i$

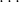
$\ldots$

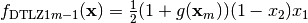
$f_{\text{DTLZ1}m-1}(\mathbf{x}) = \frac{1}{2} (1 + g(\mathbf{x}_m)) (1 - x_2) x_1$

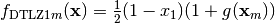
$f_{\text{DTLZ1}m}(\mathbf{x}) = \frac{1}{2} (1 - x_1)(1 + g(\mathbf{x}_m))$

Where 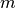$m$ is the number of objectives and 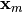$\mathbf{x}_m$ is a vector of the remaining attributes $[x_m~\ldots~x_n]$ of the individual in 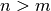$n > m$ dimensions.

deap.benchmarks.dtlz2(individual, obj)¶

DTLZ2 mutliobjective function. It returns a tuple of obj values. The individual must have at least obj elements. From: K. Deb, L. Thiele, M. Laumanns and E. Zitzler. Scalable Multi-Objective Optimization Test Problems. CEC 2002, p. 825 - 830, IEEE Press, 2002.

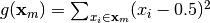
$g(\mathbf{x}_m) = \sum_{x_i \in \mathbf{x}_m} (x_i - 0.5)^2$

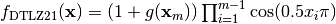
$f_{\text{DTLZ2}1}(\mathbf{x}) = (1 + g(\mathbf{x}_m)) \prod_{i=1}^{m-1} \cos(0.5x_i\pi)$

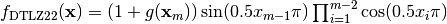
$f_{\text{DTLZ2}2}(\mathbf{x}) = (1 + g(\mathbf{x}_m)) \sin(0.5x_{m-1}\pi ) \prod_{i=1}^{m-2} \cos(0.5x_i\pi)$

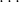
$\ldots$

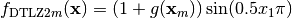
$f_{\text{DTLZ2}m}(\mathbf{x}) = (1 + g(\mathbf{x}_m)) \sin(0.5x_{1}\pi )$

Where 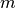$m$ is the number of objectives and 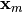$\mathbf{x}_m$ is a vector of the remaining attributes $[x_m~\ldots~x_n]$ of the individual in 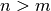$n > m$ dimensions.

deap.benchmarks.dtlz3(individual, obj)¶

DTLZ3 mutliobjective function. It returns a tuple of obj values. The individual must have at least obj elements. From: K. Deb, L. Thiele, M. Laumanns and E. Zitzler. Scalable Multi-Objective Optimization Test Problems. CEC 2002, p. 825 - 830, IEEE Press, 2002.

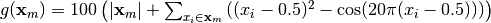
$g(\mathbf{x}_m) = 100\left(|\mathbf{x}_m| + \sum_{x_i \in \mathbf{x}_m}\left((x_i - 0.5)^2 - \cos(20\pi(x_i - 0.5))\right)\right)$

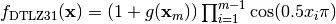
$f_{\text{DTLZ3}1}(\mathbf{x}) = (1 + g(\mathbf{x}_m)) \prod_{i=1}^{m-1} \cos(0.5x_i\pi)$

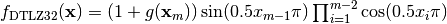
$f_{\text{DTLZ3}2}(\mathbf{x}) = (1 + g(\mathbf{x}_m)) \sin(0.5x_{m-1}\pi ) \prod_{i=1}^{m-2} \cos(0.5x_i\pi)$

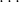
$\ldots$

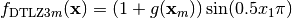
$f_{\text{DTLZ3}m}(\mathbf{x}) = (1 + g(\mathbf{x}_m)) \sin(0.5x_{1}\pi )$

Where 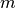$m$ is the number of objectives and 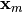$\mathbf{x}_m$ is a vector of the remaining attributes $[x_m~\ldots~x_n]$ of the individual in 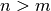$n > m$ dimensions.

deap.benchmarks.dtlz4(individual, obj, alpha)¶

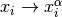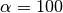DTLZ4 mutliobjective function. It returns a tuple of obj values. The individual must have at least obj elements. The alpha parameter allows for a meta-variable mapping in dtlz2() $x_i \rightarrow x_i^\alpha$ , the authors suggest $\alpha = 100$ . From: K. Deb, L. Thiele, M. Laumanns and E. Zitzler. Scalable Multi-Objective Optimization Test Problems. CEC 2002, p. 825 - 830, IEEE Press, 2002.

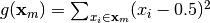
$g(\mathbf{x}_m) = \sum_{x_i \in \mathbf{x}_m} (x_i - 0.5)^2$

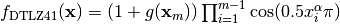
$f_{\text{DTLZ4}1}(\mathbf{x}) = (1 + g(\mathbf{x}_m)) \prod_{i=1}^{m-1} \cos(0.5x_i^\alpha\pi)$

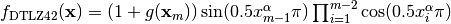
$f_{\text{DTLZ4}2}(\mathbf{x}) = (1 + g(\mathbf{x}_m)) \sin(0.5x_{m-1}^\alpha\pi ) \prod_{i=1}^{m-2} \cos(0.5x_i^\alpha\pi)$

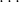
$\ldots$

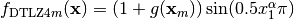
$f_{\text{DTLZ4}m}(\mathbf{x}) = (1 + g(\mathbf{x}_m)) \sin(0.5x_{1}^\alpha\pi )$

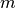Where $m$ is the number of objectives and 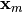$\mathbf{x}_m$ is a vector of the remaining attributes $[x_m~\ldots~x_n]$ of the individual in 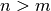$n > m$ dimensions.

deap.benchmarks.zdt1(individual)¶

ZDT1 multiobjective function

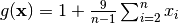
$g(\mathbf{x}) = 1 + \frac{9}{n-1}\sum_{i=2}^n x_i$

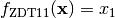
$f_{\text{ZDT1}1}(\mathbf{x}) = x_1$

$f_{\text{ZDT1}2}(\mathbf{x}) = g(\mathbf{x})\left[1 - \sqrt{\frac{x_1}{g(\mathbf{x})}}\right]$

deap.benchmarks.zdt2(individual)¶

ZDT2 multiobjective function

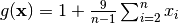
$g(\mathbf{x}) = 1 + \frac{9}{n-1}\sum_{i=2}^n x_i$

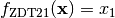
$f_{\text{ZDT2}1}(\mathbf{x}) = x_1$

$f_{\text{ZDT2}2}(\mathbf{x}) = g(\mathbf{x})\left[1 - \left(\frac{x_1}{g(\mathbf{x})}\right)^2\right]$

deap.benchmarks.zdt3(individual)¶

ZDT3 multiobjective function

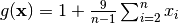
$g(\mathbf{x}) = 1 + \frac{9}{n-1}\sum_{i=2}^n x_i$

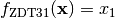
$f_{\text{ZDT3}1}(\mathbf{x}) = x_1$

$f_{\text{ZDT3}2}(\mathbf{x}) = g(\mathbf{x})\left[1 - \sqrt{\frac{x_1}{g(\mathbf{x})}} - \frac{x_1}{g(\mathbf{x})}\sin(10\pi x_1)\right]$

deap.benchmarks.zdt4(individual)¶

ZDT4 multiobjective function

$g(\mathbf{x}) = 1 + 10(n-1) + \sum_{i=2}^n \left[ x_i^2 - 10\cos(4\pi x_i) \right]$

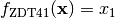
$f_{\text{ZDT4}1}(\mathbf{x}) = x_1$

$f_{\text{ZDT4}2}(\mathbf{x}) = g(\mathbf{x})\left[ 1 - \sqrt{x_1/g(\mathbf{x})} \right]$

deap.benchmarks.zdt6(individual)¶

ZDT6 multiobjective function

$g(\mathbf{x}) = 1 + 9 \left[ \left(\sum_{i=2}^n x_i\right)/(n-1) \right]^{0.25}$

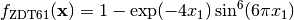
$f_{\text{ZDT6}1}(\mathbf{x}) = 1 - \exp(-4x_1)\sin^6(6\pi x_1)$

$f_{\text{ZDT6}2}(\mathbf{x}) = g(\mathbf{x}) \left[ 1 - (f_{\text{ZDT6}1}(\mathbf{x})/g(\mathbf{x}))^2 \right]$

7.2. Binary Optimization¶

deap.benchmarks.binary.chuang_f1(individual)¶

Binary deceptive function from : Multivariate Multi-Model Approach for Globally Multimodal Problems by Chung-Yao Chuang and Wen-Lian Hsu.

The function takes individual of 40+1 dimensions and has two global optima in [1,1,...,1] and [0,0,...,0].

deap.benchmarks.binary.chuang_f2(individual)¶

Binary deceptive function from : Multivariate Multi-Model Approach for Globally Multimodal Problems by Chung-Yao Chuang and Wen-Lian Hsu.

The function takes individual of 40+1 dimensions and has four global optima in [1,1,...,0,0], [0,0,...,1,1], [1,1,...,1] and [0,0,...,0].

deap.benchmarks.binary.chuang_f3(individual)¶

Binary deceptive function from : Multivariate Multi-Model Approach for Globally Multimodal Problems by Chung-Yao Chuang and Wen-Lian Hsu.

The function takes individual of 40+1 dimensions and has two global optima in [1,1,...,1] and [0,0,...,0].

deap.benchmarks.binary.royal_road1(individual, order)¶: Royal Road Function R1 as presented by Melanie Mitchell in : “An introduction to Genetic Algorithms”.

deap.benchmarks.binary.royal_road2(individual, order)¶: Royal Road Function R2 as presented by Melanie Mitchell in : “An introduction to Genetic Algorithms”.

deap.benchmarks.binary.bin2float(min_, max_, nbits)¶: Convert a binary array into an array of float where each float is composed of nbits and is between min_ and max_ and return the result of the decorated function.

Note

This decorator requires the first argument of the evaluation function to be named individual.

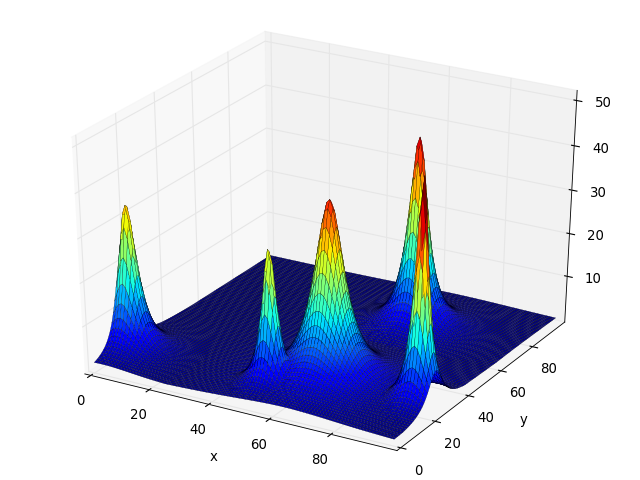
7.3. Moving Peaks Benchmark¶

Re-implementation of the Moving Peaks Benchmark by Jurgen Branke.

class deap.benchmarks.movingpeaks.MovingPeaks(self, dim[, pfunc][, npeaks][, bfunc][, random][, ...])¶

The Moving Peaks Benchmark is a fitness function changing over time. It consists of a number of peaks, changing in height, width and location. The peaks function is given by pfunc, wich is either a function object or a list of function objects (the default is function1()). The number of peaks is determined by npeaks (which defaults to 5), while the dimensionality of the search domain is dim. A basis function bfunc can also be given to act as static landscape (the default is no basis function). The argument random serves to grant an independent random number generator to the moving peaks so that the evolution is not influenced by number drawn by this object (the default uses random functions from the Python module random). Various other keyword parameters listed in the table below are required to setup the benchmark, default parameters are based on scenario 1 of this benchmark.

Parameter	`SCENARIO_1` (Default)	`SCENARIO_2`	`SCENARIO_3`	Details
`pfunc`	`function1()`	`cone()`	`cone()`	The peak function or a list of peak function.
`npeaks`	5	10	50	Number of peaks.
`bfunc`	`None`	`None`	`lambda x: 10`	Basis static function.
`min_coord`	0.0	0.0	0.0	Minimum coordinate for the centre of the peaks.
`max_coord`	100.0	100.0	100.0	Maximum coordinate for the centre of the peaks.
`min_height`	30.0	30.0	30.0	Minimum height of the peaks.
`max_height`	70.0	70.0	70.0	Maximum height of the peaks.
`uniform_height`	50.0	50.0	0	Starting height for all peaks, if `uniform_height <= 0` the initial height is set randomly for each peak.
`min_width`	0.0001	1.0	1.0	Minimum width of the peaks.
`max_width`	0.2	12.0	12.0	Maximum width of the peaks
`uniform_width`	0.1	0	0	Starting width for all peaks, if `uniform_width <= 0` the initial width is set randomly for each peak.
`lambda_`	0.0	0.5	0.5	Correlation between changes.
`move_severity`	1.0	1.5	1.0	The distance a single peak moves when peaks change.
`height_severity`	7.0	7.0	1.0	The standard deviation of the change made to the height of a peak when peaks change.
`width_severity`	0.01	1.0	0.5	The standard deviation of the change made to the width of a peak when peaks change.

Dictionnaries SCENARIO_1, SCENARIO_2 and SCENARIO_3 of this module define the defaults for these parameters. The scenario 3 requires a constant basis function which can be given as a lambda function lambda x: constant.

The following shows an example of scenario 1 with non uniform heights and widths.

(Source code, png, hires.png, pdf)

changePeaks()¶: Order the peaks to change position, height and width.

globalMaximum()¶: Returns the global maximum value and position.

maximums()¶: Returns all visible maximums value and position sorted with the global maximum first.

deap.benchmarks.movingpeaks.cone(individual, position, height, width)¶

The cone peak function to be used with scenario 2 and 3.

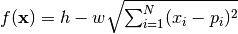
$f(\mathbf{x}) = h - w \sqrt{\sum_{i=1}^N (x_i - p_i)^2}$

deap.benchmarks.movingpeaks.function1(individual, position, height, width)¶

The function1 peak function to be used with scenario 1.

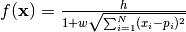
$f(\mathbf{x}) = \frac{h}{1 + w \sqrt{\sum_{i=1}^N (x_i - p_i)^2}}$

7.4. Benchmarks tools¶

Module containing tools that are useful when benchmarking algorithms

deap.benchmarks.tools.convergence(first_front, optimal_front)¶: Given a Pareto front first_front and the optimal Pareto front, this function returns a metric of convergence of the front as explained in the original NSGA-II article by K. Deb. The smaller the value is, the closer the front is to the optimal one.

deap.benchmarks.tools.diversity(first_front, first, last)¶: Given a Pareto front first_front and the two extreme points of the optimal Pareto front, this function returns a metric of the diversity of the front as explained in the original NSGA-II article by K. Deb. The smaller the value is, the better the front is.

deap.benchmarks.tools.noise(noise)¶

Decorator for evaluation functions, it evaluates the objective function and adds noise by calling the function(s) provided in the noise argument. The noise functions are called without any argument, consider using the Toolbox or Python’s functools.partial() to provide any required argument. If a single function is provided it is applied to all objectives of the evaluation function. If a list of noise functions is provided, it must be of length equal to the number of objectives. The noise argument also accept None, which will leave the objective without noise.

This decorator adds a noise() function to the decorated function.

noise.noise(noise)¶

Set the current noise to noise. After decorating the evaluation function, this function will be available directly from the function object.

prand = functools.partial(random.gauss, mu=0.0, sigma=1.0)

@noise(prand)
def evaluate(individual):
    return sum(individual),

# This will remove noise from the evaluation function
evaluate.noise(None)

deap.benchmarks.tools.rotate(matrix)¶

Decorator for evaluation functions, it rotates the objective function by matrix which should be a valid orthogonal NxN rotation matrix, with N the length of an individual. When called the decorated function should take as first argument the individual to be evaluated. The inverse rotation matrix is actually applied to the individual and the resulting list is given to the evaluation function. Thus, the evaluation function shall not be expecting an individual as it will receive a plain list (numpy.array). The multiplication is done using numpy.

This decorator adds a rotate() function to the decorated function.

Note

A random orthogonal matrix Q can be created via QR decomposition.

A = numpy.random.random((n,n))
Q, _ = numpy.linalg.qr(A)

rotate.rotate(matrix)¶

Set the current rotation to matrix. After decorating the evaluation function, this function will be available directly from the function object.

# Create a random orthogonal matrix
A = numpy.random.random((n,n))
Q, _ = numpy.linalg.qr(A)

@rotate(Q)
def evaluate(individual):
    return sum(individual),

# This will reset rotation to identity
evaluate.rotate(numpy.identity(n))

deap.benchmarks.tools.scale(factor)¶

Decorator for evaluation functions, it scales the objective function by factor which should be the same length as the individual size. When called the decorated function should take as first argument the individual to be evaluated. The inverse factor vector is actually applied to the individual and the resulting list is given to the evaluation function. Thus, the evaluation function shall not be expecting an individual as it will receive a plain list.

This decorator adds a scale() function to the decorated function.

scale.scale(factor)¶

Set the current scale to factor. After decorating the evaluation function, this function will be available directly from the function object.

@scale([0.25, 2.0, ..., 0.1])
def evaluate(individual):
    return sum(individual),

# This will cancel the scaling
evaluate.scale([1.0, 1.0, ..., 1.0])

deap.benchmarks.tools.translate(vector)¶

Decorator for evaluation functions, it translates the objective function by vector which should be the same length as the individual size. When called the decorated function should take as first argument the individual to be evaluated. The inverse translation vector is actually applied to the individual and the resulting list is given to the evaluation function. Thus, the evaluation function shall not be expecting an individual as it will receive a plain list.

This decorator adds a translate() function to the decorated function.

translate.translate(vector)¶

Set the current translation to vector. After decorating the evaluation function, this function will be available directly from the function object.

@translate([0.25, 0.5, ..., 0.1])
def evaluate(individual):
    return sum(individual),

# This will cancel the translation
evaluate.translate([0.0, 0.0, ..., 0.0])

7. Benchmarks¶

7.1. Continuous Optimization¶

7.1.1. Multi-objective¶

7.2. Binary Optimization¶

7.3. Moving Peaks Benchmark¶

7.4. Benchmarks tools¶

Table Of Contents

Previous topic

Next topic

This Page

Navigation

7. Benchmarks¶

7.1. Continuous Optimization¶

7.1.1. Multi-objective¶

7.2. Binary Optimization¶

7.3. Moving Peaks Benchmark¶

7.4. Benchmarks tools¶

Table Of Contents

Previous topic

Next topic

This Page

Quick search

Navigation