The algorithms module is intended to contain some specific algorithms in order to execute very common evolutionary algorithms. The method used here are more for convenience than reference as the implementation of every evolutionary algorithm may vary infinitely. Most of the algorithms in this module use operators registered in the toolbox. Generaly, the keyword used are mate() for crossover, mutate() for mutation, select() for selection and evaluate() for evaluation.
You are encouraged to write your own algorithms in order to make them do what you really want them to do.
These are complete boxed algorithms that are somewhat limited to the very basic evolutionary computation concepts. All algorithms accept, in addition to their arguments, an initialized Statistics object to maintain stats of the evolution, an initialized HallOfFame to hold the best individual(s) to appear in the population, and a boolean verbose to specify wether to log what is happening during the evolution or not.
This algorithm reproduce the simplest evolutionary algorithm as presented in chapter 7 of [Back2000].
| Parameters: |
|
|---|---|
| Returns: | The final population. |
It uses 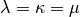 and goes as follow.
It first initializes the population (
and goes as follow.
It first initializes the population (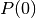 ) by evaluating
every individual presenting an invalid fitness. Then, it enters the
evolution loop that begins by the selection of the
) by evaluating
every individual presenting an invalid fitness. Then, it enters the
evolution loop that begins by the selection of the 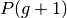 population. Then the crossover operator is applied on a proportion of
population. Then the crossover operator is applied on a proportion of
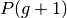 according to the cxpb probability, the resulting and the
untouched individuals are placed in
according to the cxpb probability, the resulting and the
untouched individuals are placed in 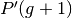 . Thereafter, a
proportion of
. Thereafter, a
proportion of 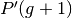 , determined by mutpb, is
mutated and placed in
, determined by mutpb, is
mutated and placed in 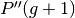 , the untouched individuals are
transferred
, the untouched individuals are
transferred 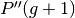 . Finally, those new individuals are evaluated
and the evolution loop continues until ngen generations are completed.
Briefly, the operators are applied in the following order
. Finally, those new individuals are evaluated
and the evolution loop continues until ngen generations are completed.
Briefly, the operators are applied in the following order
evaluate(population)
for i in range(ngen):
offspring = select(population)
offspring = mate(offspring)
offspring = mutate(offspring)
evaluate(offspring)
population = offspring
This function expects toolbox.mate(), toolbox.mutate(), toolbox.select() and toolbox.evaluate() aliases to be registered in the toolbox.
| [Back2000] | Back, Fogel and Michalewicz, “Evolutionary Computation 1 : Basic Algorithms and Operators”, 2000. |
This is the 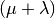 evolutionary algorithm.
evolutionary algorithm.
| Parameters: |
|
|---|---|
| Returns: | The final population. |
First, the individuals having an invalid fitness are evaluated. Then, the evolutionary loop begins by producing lambda_ offspring from the population, the offspring are generated by a crossover, a mutation or a reproduction proportionally to the probabilities cxpb, mutpb and 1 - (cxpb + mutpb). The offspring are then evaluated and the next generation population is selected from both the offspring and the population. Briefly, the operators are applied as following
evaluate(population)
for i in range(ngen):
offspring = varOr(population, toolbox, lambda_, cxpb, mutpb)
evaluate(offspring)
population = select(population + offspring, mu)
This function expects toolbox.mate(), toolbox.mutate(), toolbox.select() and toolbox.evaluate() aliases to be registered in the toolbox. This algorithm uses the varOr() variation.
This is the 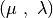 evolutionary algorithm.
evolutionary algorithm.
| Parameters: |
|
|---|---|
| Returns: | The final population. |
First, the individuals having an invalid fitness are evaluated. Then, the evolutionary loop begins by producing lambda_ offspring from the population, the offspring are generated by a crossover, a mutation or a reproduction proportionally to the probabilities cxpb, mutpb and 1 - (cxpb + mutpb). The offspring are then evaluated and the next generation population is selected only from the offspring. Briefly, the operators are applied as following
evaluate(population)
for i in range(ngen):
offspring = varOr(population, toolbox, lambda_, cxpb, mutpb)
evaluate(offspring)
population = select(offspring, mu)
This function expects toolbox.mate(), toolbox.mutate(), toolbox.select() and toolbox.evaluate() aliases to be registered in the toolbox. This algorithm uses the varOr() variation.
This is algorithm implements the ask-tell model proposed in [Colette2010], where ask is called generate and tell is called update.
| Parameters: |
|
|---|---|
| Returns: | The final population. |
The toolbox should contain a reference to the generate and the update method of the chosen strategy.
| [Colette2010] | Collette, Y., N. Hansen, G. Pujol, D. Salazar Aponte and R. Le Riche (2010). On Object-Oriented Programming of Optimizers - Examples in Scilab. In P. Breitkopf and R. F. Coelho, eds.: Multidisciplinary Design Optimization in Computational Mechanics, Wiley, pp. 527-565; |
Variations are smaller parts of the algorithms that can be used separately to build more complex algorithms.
Part of an evolutionary algorithm applying only the variation part (crossover and mutation). The modified individuals have their fitness invalidated. The individuals are cloned so returned population is independent of the input population.
| Parameters: |
|
|---|---|
| Returns: | A list of varied individuals that are independent of their parents. |
The variation goes as follow. First, the parental population
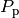 is duplicated using the toolbox.clone() method
and the result is put into the offspring population
is duplicated using the toolbox.clone() method
and the result is put into the offspring population 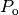 .
A first loop over
.
A first loop over 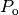 is executed to mate consecutive
individuals. According to the crossover probability cxpb, the
individuals
is executed to mate consecutive
individuals. According to the crossover probability cxpb, the
individuals 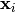 and
and 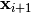 are mated
using the toolbox.mate() method. The resulting children
are mated
using the toolbox.mate() method. The resulting children
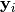 and
and 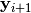 replace their respective
parents in
replace their respective
parents in 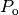 . A second loop over the resulting
. A second loop over the resulting
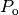 is executed to mutate every individual with a
probability mutpb. When an individual is mutated it replaces its not
mutated version in
is executed to mutate every individual with a
probability mutpb. When an individual is mutated it replaces its not
mutated version in 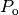 . The resulting
. The resulting
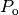 is returned.
is returned.
This variation is named And beceause of its propention to apply both
crossover and mutation on the individuals. Note that both operators are
not applied systematicaly, the resulting individuals can be generated from
crossover only, mutation only, crossover and mutation, and reproduction
according to the given probabilities. Both probabilities should be in
![[0, 1]](../_images/math/787ef8897f85416cae83d74ef5630a9c5973d996.png) .
.
Part of an evolutionary algorithm applying only the variation part (crossover, mutation or reproduction). The modified individuals have their fitness invalidated. The individuals are cloned so returned population is independent of the input population.
| Parameters: |
|
|---|---|
| Returns: | A list of varied individuals that are independent of their parents. |
The variation goes as follow. On each of the lambda_ iteration, it
selects one of the three operations; crossover, mutation or reproduction.
In the case of a crossover, two individuals are selected at random from
the parental population 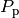 , those individuals are cloned
using the toolbox.clone() method and then mated using the
toolbox.mate() method. Only the first child is appended to the
offspring population
, those individuals are cloned
using the toolbox.clone() method and then mated using the
toolbox.mate() method. Only the first child is appended to the
offspring population 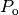 , the second child is discarded.
In the case of a mutation, one individual is selected at random from
, the second child is discarded.
In the case of a mutation, one individual is selected at random from
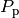 , it is cloned and then mutated using using the
toolbox.mutate() method. The resulting mutant is appended to
, it is cloned and then mutated using using the
toolbox.mutate() method. The resulting mutant is appended to
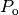 . In the case of a reproduction, one individual is
selected at random from
. In the case of a reproduction, one individual is
selected at random from 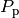 , cloned and appended to
, cloned and appended to
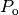 .
.
This variation is named Or beceause an offspring will never result from
both operations crossover and mutation. The sum of both probabilities
shall be in ![[0, 1]](../_images/math/787ef8897f85416cae83d74ef5630a9c5973d996.png) , the reproduction probability is
1 - cxpb - mutpb.
, the reproduction probability is
1 - cxpb - mutpb.
A module that provides support for the Covariance Matrix Adaptation Evolution Strategy.
A strategy that will keep track of the basic parameters of the CMA-ES algorithm.
| Parameters: |
|
|---|
| Parameter | Default | Details |
|---|---|---|
| lambda_ | int(4 + 3 * log(N)) | Number of children to produce at each generation, N is the individual’s size (integer). |
| mu | int(lambda_ / 2) | The number of parents to keep from the lambda children (integer). |
| cmatrix | identity(N) | The initial covariance matrix of the distribution that will be sampled. |
| weights | "superlinear" | Decrease speed, can be "superlinear", "linear" or "equal". |
| cs | (mueff + 2) / (N + mueff + 3) | Cumulation constant for step-size. |
| damps | 1 + 2 * max(0, sqrt(( mueff - 1) / (N + 1)) - 1) + cs | Damping for step-size. |
| ccum | 4 / (N + 4) | Cumulation constant for covariance matrix. |
| ccov1 | 2 / ((N + 1.3)^2 + mueff) | Learning rate for rank-one update. |
| ccovmu | 2 * (mueff - 2 + 1 / mueff) / ((N + 2)^2 + mueff) | Learning rate for rank-mu update. |
Computes the parameters depending on 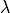 . It needs to
be called again if
. It needs to
be called again if 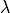 changes during evolution.
changes during evolution.
| Parameters: | params – A dictionary of the manually set parameters. |
|---|
Generate a population of 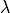 individuals of type
ind_init from the current strategy.
individuals of type
ind_init from the current strategy.
| Parameters: | ind_init – A function object that is able to initialize an individual from a list. |
|---|---|
| Returns: | A list of individuals. |
Update the current covariance matrix strategy from the population.
| Parameters: | population – A list of individuals from which to update the parameters. |
|---|
A CMA-ES strategy that uses the 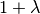 paradigme.
paradigme.
| Parameters: |
|
|---|
Computes the parameters depending on 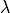 . It needs to
be called again if
. It needs to
be called again if 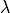 changes during evolution.
changes during evolution.
| Parameters: | params – A dictionary of the manually set parameters. |
|---|
Generate a population of 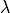 individuals of type
ind_init from the current strategy.
individuals of type
ind_init from the current strategy.
| Parameters: | ind_init – A function object that is able to initialize an individual from a list. |
|---|---|
| Returns: | A list of individuals. |
Update the current covariance matrix strategy from the population.
| Parameters: | population – A list of individuals from which to update the parameters. |
|---|