2. Evolutionary Tools¶

The tools module contains the operators for evolutionary algorithms. They are used to modify, select and move the individuals in their environment. The set of operators it contains are readily usable in the Toolbox. In addition to the basic operators this module also contains utility tools to enhance the basic algorithms with Statistics, HallOfFame, Checkpoint, and History.

2.1. Operators¶

The operator set does the minimum job for transforming or selecting individuals. This means, for example, that providing two individuals to the crossover will transform those individuals in-place. The responsibility of making offspring(s) independent of their parent(s) and invalidating the fitness is left to the user and is generally fulfilled in the algorithms by calling toolbox.clone() on an individual to duplicate it and del on the values attribute of the individual’s fitness to invalidate it.

Here is a list of the implemented operators in DEAP,

Initialization	Crossover	Mutation	Selection	Migration
`initRepeat()`	`cxOnePoint()`	`mutGaussian()`	`selTournament()`	`migRing()`
`initIterate()`	`cxTwoPoints()`	`mutShuffleIndexes()`	`selRoulette()`
`initCycle()`	`cxUniform()`	`mutFlipBit()`	`selNSGA2()`
	`cxPartialyMatched()`	`mutPolynomialBounded()`	`selSPEA2()`
	`cxUniformPartialyMatched()`	`mutUniformInt()`	`selRandom()`
	`cxOrdered()`	`mutESLogNormal()`	`selBest()`
	`cxBlend()`		`selWorst()`
	`cxESBlend()`		`selTournamentDCD()`
	`cxESTwoPoints()`		`selDoubleTournament()`
	`cxSimulatedBinary()`
	`cxSimulatedBinaryBounded()`
	`cxMessyOnePoint()`

and genetic programming specific operators.

Initialization	Crossover	Mutation	Bloat control
`genFull()`	`cxOnePoint()`	`mutShrink()`	`staticDepthLimit()`
`genGrow()`	`cxOnePointLeafBiased()`	`mutUniform()`	`staticSizeLimit()`
`genRamped()`		`mutNodeReplacement()`	`selDoubleTournament()`
		`mutEphemeral()`
		`mutInsert()`

2.1.1. Initialization¶

deap.tools.initRepeat(container, func, n)¶

Call the function container with a generator function corresponding to the calling n times the function func.

Parameters:	container – The type to put in the data from func. func – The function that will be called n times to fill the container. n – The number of times to repeat func.
Returns:	An instance of the container filled with data from func.

This helper function can can be used in conjunction with a Toolbox to register a generator of filled containers, as individuals or population.

>>> initRepeat(list, random.random, 2) 
...                                    
[0.4761..., 0.6302...]

See the List of Floats and Population tutorials for more examples.

deap.tools.initIterate(container, generator)¶

Call the function container with an iterable as its only argument. The iterable must be returned by the method or the object generator.

Parameters:	container – The type to put in the data from func. generator – A function returning an iterable (list, tuple, ...), the content of this iterable will fill the container.
Returns:	An instance of the container filled with data from the generator.

This helper function can can be used in conjunction with a Toolbox to register a generator of filled containers, as individuals or population.

>>> from random import sample
>>> from functools import partial
>>> gen_idx = partial(sample, range(10), 10)
>>> initIterate(list, gen_idx)
[4, 5, 3, 6, 0, 9, 2, 7, 1, 8]

See the Permutation and Arithmetic Expression tutorials for more examples.

deap.tools.initCycle(container, seq_func, n=1)¶

Call the function container with a generator function corresponding to the calling n times the functions present in seq_func.

Parameters:	container – The type to put in the data from func. seq_func – A list of function objects to be called in order to fill the container. n – Number of times to iterate through the list of functions.
Returns:	An instance of the container filled with data from the returned by the functions.

This helper function can can be used in conjunction with a Toolbox to register a generator of filled containers, as individuals or population.

>>> func_seq = [lambda:1 , lambda:'a', lambda:3]
>>> initCycle(list, func_seq, n=2)
[1, 'a', 3, 1, 'a', 3]

See the A Funky One tutorial for an example.

deap.gp.genFull(pset, min_, max_, type_=None)¶

Generate an expression where each leaf has a the same depth between min and max.

Parameters:	pset – A primitive set from wich to select primitives of the trees. min – Minimum height of the produced trees. max – Maximum Height of the produced trees. type – The type that should return the tree when called, when `None` (default) no return type is enforced.
Returns:	A full tree with all leaves at the same depth.

deap.gp.genGrow(pset, min_, max_, type_=None)¶

Generate an expression where each leaf might have a different depth between min and max.

Parameters:	pset – A primitive set from wich to select primitives of the trees. min – Minimum height of the produced trees. max – Maximum Height of the produced trees. type – The type that should return the tree when called, when `None` (default) no return type is enforced.
Returns:	A grown tree with leaves at possibly different depths.

deap.gp.genRamped(pset, min_, max_, type_=None)¶

Generate an expression with a PrimitiveSet pset. Half the time, the expression is generated with genGrow(), the other half, the expression is generated with genFull().

Parameters:	pset – A primitive set from wich to select primitives of the trees. min – Minimum height of the produced trees. max – Maximum Height of the produced trees. type – The type that should return the tree when called, when `None` (default) no return type is enforced.
Returns:	Either, a full or a grown tree.

2.1.2. Crossover¶

deap.tools.cxOnePoint(ind1, ind2)¶

Execute a one point crossover on the input individuals. The two individuals are modified in place. The resulting individuals will respectively have the length of the other.

Parameters:	ind1 – The first individual participating in the crossover. ind2 – The second individual participating in the crossover.
Returns:	A tuple of two individuals.

This function use the randint() function from the python base random module.

deap.tools.cxTwoPoints(ind1, ind2)¶

Execute a two points crossover on the input individuals. The two individuals are modified in place and both keep their original length.

Parameters:	ind1 – The first individual participating in the crossover. ind2 – The second individual participating in the crossover.
Returns:	A tuple of two individuals.

This function use the randint() function from the python base random module.

deap.tools.cxUniform(ind1, ind2, indpb)¶

Execute a uniform crossover that modify in place the two individuals. The attributes are swapped according to the indpb probability.

Parameters:	ind1 – The first individual participating in the crossover. ind2 – The second individual participating in the crossover. indpb – Independent probabily for each attribute to be exchanged.
Returns:	A tuple of two individuals.

This function use the random() function from the python base random module.

deap.tools.cxPartialyMatched(ind1, ind2)¶

Execute a partially matched crossover (PMX) on the input individuals. The two individuals are modified in place. This crossover expect iterable individuals of indices, the result for any other type of individuals is unpredictable.

Parameters:	ind1 – The first individual participating in the crossover. ind2 – The second individual participating in the crossover.
Returns:	A tuple of two individuals.

Moreover, this crossover consists of generating two children by matching pairs of values in a certain range of the two parents and swapping the values of those indexes. For more details see [Goldberg1985].

This function use the randint() function from the python base random module.

[Goldberg1985]

Goldberg and Lingel, “Alleles, loci, and the traveling salesman problem”, 1985.

deap.tools.cxUniformPartialyMatched(ind1, ind2, indpb)¶

Execute a uniform partially matched crossover (UPMX) on the input individuals. The two individuals are modified in place. This crossover expect iterable individuals of indices, the result for any other type of individuals is unpredictable.

Parameters:	ind1 – The first individual participating in the crossover. ind2 – The second individual participating in the crossover.
Returns:	A tuple of two individuals.

Moreover, this crossover consists of generating two children by matching pairs of values chosen at random with a probability of indpb in the two parents and swapping the values of those indexes. For more details see [Cicirello2000].

This function use the random() and randint() functions from the python base random module.

[Cicirello2000]

Cicirello and Smith, “Modeling GA performance for control parameter optimization”, 2000.

deap.tools.cxOrdered(ind1, ind2)¶

Execute an ordered crossover (OX) on the input individuals. The two individuals are modified in place. This crossover expect iterable individuals of indices, the result for any other type of individuals is unpredictable.

Parameters:	ind1 – The first individual participating in the crossover. ind2 – The second individual participating in the crossover.
Returns:	A tuple of two individuals.

Moreover, this crossover consists of generating holes in the input individuals. A hole is created when an attribute of an individual is between the two crossover points of the other individual. Then it rotates the element so that all holes are between the crossover points and fills them with the removed elements in order. For more details see [Goldberg1989].

This function use the sample() function from the python base random module.

[Goldberg1989]

Goldberg. Genetic algorithms in search, optimization and machine learning. Addison Wesley, 1989

deap.tools.cxBlend(ind1, ind2, alpha)¶

Executes a blend crossover that modify in-place the input individuals. The blend crossover expect individuals formed of a list of floating point numbers.

Parameters:	ind1 – The first individual participating in the crossover. ind2 – The second individual participating in the crossover. alpha – Extent of the interval in which the new values can be drawn for each attribute on both side of the parents’ attributes.
Returns:	A tuple of two individuals.

This function use the random() function from the python base random module.

deap.tools.cxESBlend(ind1, ind2, alpha)¶

Execute a blend crossover on both, the individual and the strategy. The individuals must have a strategy attribute. Adjustement of the minimal strategy shall be done after the call to this function, consider using a decorator.

Parameters:	ind1 – The first evolution strategy participating in the crossover. ind2 – The second evolution strategy participating in the crossover. alpha – Extent of the interval in which the new values can be drawn for each attribute on both side of the parents’ attributes.
Returns:	A tuple of two evolution strategies.

deap.tools.cxESTwoPoints(ind1, ind2)¶

Execute a classical two points crossover on both the individual and its strategy. The individuals must have a strategy attribute.The crossover points for the individual and the strategy are the same.

Parameters:	ind1 – The first evolution strategy participating in the crossover. ind2 – The second evolution strategy participating in the crossover.
Returns:	A tuple of two evolution strategies.

deap.tools.cxSimulatedBinary(ind1, ind2, eta)¶

Executes a simulated binary crossover that modify in-place the input individuals. The simulated binary crossover expect individuals formed of a list of floating point numbers.

Parameters:	ind1 – The first individual participating in the crossover. ind2 – The second individual participating in the crossover. eta – Crowding degree of the crossover. A high eta will produce children resembling to their parents, while a small eta will produce solutions much more different.
Returns:	A tuple of two individuals.

This function use the random() function from the python base random module.

deap.tools.cxSimulatedBinaryBounded(ind1, ind2, eta, low, up)¶

Executes a simulated binary crossover that modify in-place the input individuals. The simulated binary crossover expect individuals formed of a list of floating point numbers.

Parameters:

ind1 – The first individual participating in the crossover.
ind2 – The second individual participating in the crossover.
eta – Crowding degree of the crossover. A high eta will produce children resembling to their parents, while a small eta will produce solutions much more different.
low – A value or a sequence of values that is the lower bound of the search space.
up – A value or a sequence of values that is the upper bound of the search space.

Returns:

A tuple of two individuals.

This function use the random() function from the python base random module.

Note

This implementation is similar to the one implemented in the original NSGA-II C code presented by Deb.

deap.tools.cxMessyOnePoint(ind1, ind2)¶

Execute a one point crossover that will in most cases change the individuals size. The two individuals are modified in place.

Parameters:	ind1 – The first individual participating in the crossover. ind2 – The second individual participating in the crossover.
Returns:	A tuple of two individuals.

This function use the randint() function from the python base random module.

deap.gp.cxOnePoint(ind1, ind2)¶

Randomly select in each individual and exchange each subtree with the point as root between each individual.

Parameters:	ind1 – First tree participating in the crossover. ind2 – Second tree participating in the crossover.
Returns:	A tuple of two trees.

deap.gp.cxOnePointLeafBiased(ind1, ind2, termpb)¶

Randomly select crossover point in each individual and exchange each subtree with the point as root between each individual.

Parameters:	ind1 – First typed tree participating in the crossover. ind2 – Second typed tree participating in the crossover. termpb – The probability of chosing a terminal node (leaf).
Returns:	A tuple of two typed trees.

When the nodes are strongly typed, the operator makes sure the second node type corresponds to the first node type.

The parameter termpb sets the probability to choose between a terminal or non-terminal crossover point. For instance, as defined by Koza, non- terminal primitives are selected for 90% of the crossover points, and terminals for 10%, so termpb should be set to 0.1.

2.1.3. Mutation¶

deap.tools.mutGaussian(individual, mu, sigma, indpb)¶

This function applies a gaussian mutation of mean mu and standard deviation sigma on the input individual. This mutation expects an iterable individual composed of real valued attributes. The indpb argument is the probability of each attribute to be mutated.

Parameters:	individual – Individual to be mutated. mu – Mean around the individual of the mutation. sigma – Standard deviation of the mutation. indpb – Probability for each attribute to be mutated.
Returns:	A tuple of one individual.

This function uses the random() and gauss() functions from the python base random module.

deap.tools.mutShuffleIndexes(individual, indpb)¶

Shuffle the attributes of the input individual and return the mutant. The individual is expected to be iterable. The indpb argument is the probability of each attribute to be moved. Usually this mutation is applied on vector of indices.

Parameters:	individual – Individual to be mutated. indpb – Probability for each attribute to be exchanged to another position.
Returns:	A tuple of one individual.

This function uses the random() and randint() functions from the python base random module.

deap.tools.mutFlipBit(individual, indpb)¶

Flip the value of the attributes of the input individual and return the mutant. The individual is expected to be iterable and the values of the attributes shall stay valid after the not operator is called on them. The indpb argument is the probability of each attribute to be flipped. This mutation is usually applied on boolean individuals.

Parameters:	individual – Individual to be mutated. indpb – Probability for each attribute to be flipped.
Returns:	A tuple of one individual.

This function uses the random() function from the python base random module.

deap.tools.mutUniformInt(individual, low, up, indpb)¶

Mutate an individual by replacing attributes, with probability indpb, by a integer uniformly drawn between low and up inclusively.

Parameters:	low – The lower bound of the range from wich to draw the new integer. up – The upper bound of the range from wich to draw the new integer. indpb – Probability for each attribute to be mutated.
Returns:	A tuple of one individual.

deap.tools.mutPolynomialBounded(individual, eta, low, up, indpb)¶

Polynomial mutation as implemented in original NSGA-II algorithm in C by Deb.

Parameters:	individual – Individual to be mutated. eta – Crowding degree of the mutation. A high eta will produce a mutant resembling its parent, while a small eta will produce a solution much more different. low – A value or a sequence of values that is the lower bound of the search space. up – A value or a sequence of values that is the upper bound of the search space.
Returns:	A tuple of one individual.

deap.tools.mutESLogNormal(individual, c, indpb)¶

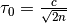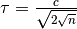Mutate an evolution strategy according to its strategy attribute as described in [Beyer2002]. First the strategy is mutated according to an extended log normal rule, $\boldsymbol{\sigma}_t = \exp(\tau_0 \mathcal{N}_0(0, 1)) \left[ \sigma_{t-1, 1}\exp(\tau \mathcal{N}_1(0, 1)), \ldots, \sigma_{t-1, n} \exp(\tau \mathcal{N}_n(0, 1))\right]$ , with $\tau_0 = \frac{c}{\sqrt{2n}}$ and $\tau = \frac{c}{\sqrt{2\sqrt{n}}}$ , the the individual is mutated by a normal distribution of mean 0 and standard deviation of $\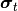boldsymbol{\sigma}_{t}$ (its current strategy) then . A recommended choice is c=1 when using a $(10, 100)$ evolution strategy [Beyer2002] [Schwefel1995].

Parameters:	individual – Individual to be mutated. c – The learning parameter. indpb – Probability for each attribute to be flipped.
Returns:	A tuple of one individual.

[Beyer2002]

(1, 2) Beyer and Schwefel, 2002, Evolution strategies - A Comprehensive Introduction

[Schwefel1995]

Schwefel, 1995, Evolution and Optimum Seeking. Wiley, New York, NY

deap.gp.mutShrink(individual)¶

This operator shrinks the individual by chosing randomly a branch and replacing it with one of the branch’s arguments (also randomly chosen).

Parameters:	individual – The tree to be shrinked.
Returns:	A tuple of one tree.

deap.gp.mutUniform(individual, expr)¶

Randomly select a point in the tree individual, then replace the subtree at that point as a root by the expression generated using method expr().

Parameters:	individual – The tree to be mutated. expr – A function object that can generate an expression when called.
Returns:	A tuple of one tree.

deap.gp.mutNodeReplacement(individual)¶

Replaces a randomly chosen primitive from individual by a randomly chosen primitive with the same number of arguments from the pset attribute of the individual.

Parameters:	individual – The normal or typed tree to be mutated.
Returns:	A tuple of one tree.

deap.gp.mutEphemeral(individual, mode)¶

This operator works on the constants of the tree individual. In mode "one", it will change the value of one of the individual ephemeral constants by calling its generator function. In mode "all", it will change the value of all the ephemeral constants.

Parameters:	individual – The normal or typed tree to be mutated. mode – A string to indicate to change `"one"` or `"all"` ephemeral constants.
Returns:	A tuple of one tree.

deap.gp.mutInsert(individual)¶

Inserts a new branch at a random position in individual. The subtree at the chosen position is used as child node of the created subtree, in that way, it is really an insertion rather than a replacement. Note that the original subtree will become one of the children of the new primitive inserted, but not perforce the first (its position is randomly selected if the new primitive has more than one child).

Parameters:	individual – The normal or typed tree to be mutated.
Returns:	A tuple of one tree.

2.1.4. Selection¶

deap.tools.selTournament(individuals, k, tournsize)¶

Select k individuals from the input individuals using k tournaments of tournsize individuals. The list returned contains references to the input individuals.

Parameters:	individuals – A list of individuals to select from. k – The number of individuals to select. tournsize – The number of individuals participating in each tournament.
Returns:	A list of selected individuals.

This function uses the choice() function from the python base random module.

deap.tools.selRoulette(individuals, k)¶

Select k individuals from the input individuals using k spins of a roulette. The selection is made by looking only at the first objective of each individual. The list returned contains references to the input individuals.

Parameters:	individuals – A list of individuals to select from. k – The number of individuals to select.
Returns:	A list of selected individuals.

This function uses the random() function from the python base random module.

Warning

The roulette selection by definition cannot be used for minimization or when the fitness can be smaller or equal to 0.

deap.tools.selNSGA2(individuals, k)¶

Apply NSGA-II selection operator on the individuals. Usually, the size of individuals will be larger than k because any individual present in individuals will appear in the returned list at most once. Having the size of individuals equals to k will have no effect other than sorting the population according to a non-domination scheme. The list returned contains references to the input individuals. For more details on the NSGA-II operator see [Deb2002].

Parameters:	individuals – A list of individuals to select from. k – The number of individuals to select.
Returns:	A list of selected individuals.

[Deb2002]

Deb, Pratab, Agarwal, and Meyarivan, “A fast elitist non-dominated sorting genetic algorithm for multi-objective optimization: NSGA-II”, 2002.

deap.tools.selSPEA2(individuals, k)¶

Apply SPEA-II selection operator on the individuals. Usually, the size of individuals will be larger than n because any individual present in individuals will appear in the returned list at most once. Having the size of individuals equals to n will have no effect other than sorting the population according to a strength Pareto scheme. The list returned contains references to the input individuals. For more details on the SPEA-II operator see [Zitzler2001].

Parameters:	individuals – A list of individuals to select from. k – The number of individuals to select.
Returns:	A list of selected individuals.

[Zitzler2001]

Zitzler, Laumanns and Thiele, “SPEA 2: Improving the strength Pareto evolutionary algorithm”, 2001.

deap.tools.selRandom(individuals, k)¶

Select k individuals at random from the input individuals with replacement. The list returned contains references to the input individuals.

Parameters:	individuals – A list of individuals to select from. k – The number of individuals to select.
Returns:	A list of selected individuals.

This function uses the choice() function from the python base random module.

deap.tools.selBest(individuals, k)¶

Select the k best individuals among the input individuals. The list returned contains references to the input individuals.

Parameters:	individuals – A list of individuals to select from. k – The number of individuals to select.
Returns:	A list containing the k best individuals.

deap.tools.selWorst(individuals, k)¶

Select the k worst individuals among the input individuals. The list returned contains references to the input individuals.

Parameters:	individuals – A list of individuals to select from. k – The number of individuals to select.
Returns:	A list containing the k worst individuals.

deap.tools.selDoubleTournament(individuals, k, fitness_size, parsimony_size, fitness_first)¶

Tournament selection which use the size of the individuals in order to discriminate good solutions. This kind of tournament is obviously useless with fixed-length representation, but has been shown to significantly reduce excessive growth of individuals, especially in GP, where it can be used as a bloat control technique (see [Luke2002fighting]). This selection operator implements the double tournament technique presented in this paper.

The core principle is to use a normal tournament selection, but using a special sample function to select aspirants, which is another tournament based on the size of the individuals. To ensure that the selection pressure is not too high, the size of the size tournament (the number of candidates evaluated) can be a real number between 1 and 2. In this case, the smaller individual among two will be selected with a probability size_tourn_size/2. For instance, if size_tourn_size is set to 1.4, then the smaller individual will have a 0.7 probability to be selected.

Note

In GP, it has been shown that this operator produces better results when it is combined with some kind of a depth limit.

Parameters:

individuals – A list of individuals to select from.
k – The number of individuals to select.
fitness_size – The number of individuals participating in each fitness tournament
parsimony_size – The number of individuals participating in each size tournament. This value has to be a real number in the range [1,2], see above for details.
fitness_first – Set this to True if the first tournament done should be the fitness one (i.e. the fitness tournament producing aspirants for the size tournament). Setting it to False will behaves as the opposite (size tournament feeding fitness tournaments with candidates). It has been shown that this parameter does not have a significant effect in most cases (see [Luke2002fighting]).

Returns:

A list of selected individuals.

[Luke2002fighting]

(1, 2) Luke and Panait, 2002, Fighting bloat with nonparametric parsimony pressure

deap.tools.selTournamentDCD(individuals, k)¶

Tournament selection based on dominance (D) between two individuals, if the two individuals do not interdominate the selection is made based on crowding distance (CD). The individuals sequence length has to be a multiple of 4. Starting from the beginning of the selected individuals, two consecutive individuals will be different (assuming all individuals in the input list are unique). Each individual from the input list won’t be selected more than twice.

This selection requires the individuals to have a crowding_dist attribute, which can be set by the assignCrowdingDist() function.

Parameters:	individuals – A list of individuals to select from. k – The number of individuals to select.
Returns:	A list of selected individuals.

deap.tools.sortFastND(individuals, k, first_front_only=False)¶

Sort the first k individuals according the the fast non-dominated sorting algorithm.

Parameters:	individuals – A list of individuals to select from. k – The number of individuals to select. first_front_only – If `True` sort only the first front and exit.
Returns:	A list of Pareto fronts (lists), with the first list being the true Pareto front.

deap.tools.assignCrowdingDist(individuals)¶: Assign a crowding distance to each individual of the list. The crowding distance is set to the crowding_dist attribute of each individual.

2.1.5. Bloat control¶

deap.gp.staticDepthLimit(max_depth)¶

Implement a static limit on the depth of a GP tree, as defined by Koza in [Koza1989]. It may be used to decorate both crossover and mutation operators. When an invalid (too high) child is generated, it is simply replaced by one of its parents.

This operator can be used to avoid memory errors occuring when the tree gets higher than 90-95 levels (as Python puts a limit on the call stack depth), because it ensures that no tree higher than max_depth will ever be accepted in the population (except if it was generated at initialization time).

Parameters:	max_depth – The maximum depth allowed for an individual.
Returns:	A decorator that can be applied to a GP operator using `decorate()`

Note

If you want to reproduce the exact behavior intended by Koza, set the max_depth param to 17.

[Koza1989]

J.R. Koza, Genetic Programming - On the Programming of Computers by Means of Natural Selection (MIT Press, Cambridge, MA, 1992)

deap.gp.staticSizeLimit(max_size)¶

Implement a static limit on the size of a GP tree. It may be used to decorate both crossover and mutation operators. When an invalid (too big) child is generated, it is simply replaced by one of its parents.

Parameters:	max_size – The maximum size (number of nodes) allowed for an individual
Returns:	A decorator that can be applied to a GP operator using `decorate()`

2.1.6. Migration¶

deap.tools.migRing(populations, k, selection[, replacement, migarray])¶

Perform a ring migration between the populations. The migration first select k emigrants from each population using the specified selection operator and then replace k individuals from the associated population in the migarray by the emigrants. If no replacement operator is specified, the immigrants will replace the emigrants of the population, otherwise, the immigrants will replace the individuals selected by the replacement operator. The migration array, if provided, shall contain each population’s index once and only once. If no migration array is provided, it defaults to a serial ring migration (1 – 2 – ... – n – 1). Selection and replacement function are called using the signature selection(populations[i], k) and replacement(populations[i], k). It is important to note that the replacement strategy must select k different individuals. For example, using a traditional tournament for replacement strategy will thus give undesirable effects, two individuals will most likely try to enter the same slot.

Parameters:

populations – A list of (sub-)populations on which to operate migration.
k – The number of individuals to migrate.
selection – The function to use for selection.
replacement – The function to use to select which individuals will be replaced. If None (default) the individuals that leave the population are directly replaced.
migarray – A list of indices indicating where the individuals from a particular position in the list goes. This defaults to a ring migration.

2.2. Statistics¶

class deap.tools.Statistics([key][, n])¶

A statistics object that holds the required data for as long as it exists. When created the statistics object receives a key argument that is used to get the required data, if not provided the key argument defaults to the identity function. A statistics object can be represented as multiple 3 dimensional matrix, for each registered function there is a matrix.

Parameters:	key – A function to access the data on which to compute the statistics, optional. n – The number of independent statistics to maintain in this statistics object.

Along the first axis (wich length is given by the n argument) are independent statistics on different collections given this index in the update() method. The second is the accumulator of statistics, each time the update function is called the new statistics are added using the registered functions at the end of this axis. The third axis is used when the entered data is an iterable (for example a multiobjective fitness).

Data can be retrieved by accessing the statistic function name followed by the indicices of the element we wish to access.

>>> s = Statistics(n=2)
>>> s.register("Mean", mean)
>>> s.update([1, 2, 3, 4], index=0)
>>> s.update([5, 6, 7, 8], index=1)
>>> s.Mean[0][-1]
[2.5]
>>> s.Mean[1][-1]
[6.5]
>>> s.update([10, 20, 30, 40], index=0)
>>> s.update([50, 60, 70, 80], index=1)
>>> s.Mean[0][1]
[25.0]
>>> s.Mean[1][1]
[65.0]

register(name, function)¶

Register a function function that will be apply on the sequence each time update() is called.

Parameters:	name – The name of the statistics function as it would appear in the dictionnary of the statistics object. function – A function that will compute the desired statistics on the data as preprocessed by the key.

The function result will be accessible by using the string given by the argument name as a function of the statistics object.

>>> s = Statistics()
>>> s.register("Mean", mean)
>>> s.update([1,2,3,4,5,6,7])
>>> s.Mean
[[[4.0]]]

update(seq, index=0, add=False)¶

Apply to the input sequence seq each registered function and store each result in a list specific to the function and the data index index.

Parameters:

seq – A sequence on which the key will be applied to get the data.
index – The index of the independent statistics object in which to add the computed statistics, optional (defaults to 0).
add – A boolean to force adding depth to the statistics object when the index is out of range. If the given index is not yet registered, it adds it to the statistics only if it is one greater than the larger index, optional (defaults to False).

>>> s = Statistics()
>>> s.register("Mean", mean)
>>> s.register("Max", max)
>>> s.update([4,5,6,7,8])
>>> s.Max
[[[8]]]
>>> s.Mean
[[[6.0]]]
>>> s.update([1,2,3])
>>> s.Max
[[[8], [3]]]

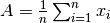deap.tools.mean(seq)¶: Returns the arithmetic mean of the sequence seq = $\{x_1,\ldots,x_n\}$ as $A = \frac{1}{n} \sum_{i=1}^n x_i$ .

deap.tools.median(seq)¶: Returns the median of seq - the numeric value separating the higher half of a sample from the lower half. If there is an even number of elements in seq, it returns the mean of the two middle values.

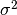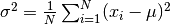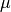deap.tools.var(seq)¶: Returns the variance $\sigma^2$ of seq = $\{x_1,\ldots,x_n\}$ as $\sigma^2 = \frac{1}{N} \sum_{i=1}^N (x_i - \mu )^2$ , where $\mu$ is the arithmetic mean of seq.

deap.tools.std(seq)¶: Returns the square root of the variance 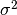$\sigma^2$ of seq.

2.3. Hall-Of-Fame¶

class deap.tools.HallOfFame(maxsize)¶

The hall of fame contains the best individual that ever lived in the population during the evolution. It is sorted at all time so that the first element of the hall of fame is the individual that has the best first fitness value ever seen, according to the weights provided to the fitness at creation time.

Parameters:	maxsize – The maximum number of individual to keep in the hall of fame.

The class HallOfFame provides an interface similar to a list (without being one completely). It is possible to retrieve its length, to iterate on it forward and backward and to get an item or a slice from it.

update(population)¶

Update the hall of fame with the population by replacing the worst individuals in it by the best individuals present in population (if they are better). The size of the hall of fame is kept constant.

Parameters:	population – A list of individual with a fitness attribute to update the hall of fame with.

insert(item)¶

Insert a new individual in the hall of fame using the bisect_right() function. The inserted individual is inserted on the right side of an equal individual. Inserting a new individual in the hall of fame also preserve the hall of fame’s order. This method does not check for the size of the hall of fame, in a way that inserting a new individual in a full hall of fame will not remove the worst individual to maintain a constant size.

Parameters:	item – The individual with a fitness attribute to insert in the hall of fame.

remove(index)¶

Remove the specified index from the hall of fame.

Parameters:	index – An integer giving which item to remove.

clear()¶: Clear the hall of fame.

class deap.tools.ParetoFront([similar])¶

The Pareto front hall of fame contains all the non-dominated individuals that ever lived in the population. That means that the Pareto front hall of fame can contain an infinity of different individuals.

Parameters:	similar – A function that tels the Pareto front whether or not two individuals are similar, optional.

The size of the front may become very large if it is used for example on a continuous function with a continuous domain. In order to limit the number of individuals, it is possible to specify a similarity function that will return True if the genotype of two individuals are similar. In that case only one of the two individuals will be added to the hall of fame. By default the similarity function is operator.__eq__().

Since, the Pareto front hall of fame inherits from the HallOfFame, it is sorted lexicographically at every moment.

update(population)¶

Update the Pareto front hall of fame with the population by adding the individuals from the population that are not dominated by the hall of fame. If any individual in the hall of fame is dominated it is removed.

Parameters:	population – A list of individual with a fitness attribute to update the hall of fame with.

2.4. Evolution Logger¶

class deap.tools.EvolutionLogger([col_names][, precision])¶

The evolution logger logs data about the evolution to either the stdout or a file. To change the destination of the logger simply change its attribute output to an filestream. The columns argument provides the data column to log when using statistics, the names should be identical to what is registered in the statistics object (it default to [“gen”, “evals”] wich will log the generation number and the number of evaluated individuals). When logging with function logGeneration(), the provided columns must be given either as arguments or in the statistics object. The precision indicates the precision to use when logging statistics.

Parameters:	columns – A list of strings of the name of the data as it will appear in the statistics object, optional. precision – Number of decimal digits to log, optional.

logHeader()¶: Logs the column titles specified during initialization.

logGeneration([stats[, index]][, data[, ...]])¶

Logs the registered generation identifiers given a columns on initialization. Each element of the columns must be provided either in the stats object or as keyword argument. When loggin through the stats object, the last entry of the data under the column names at index is logged (index defaults to 0).

Parameters:	stats – A statistics object containing the data to log, optional. index – The index in the statistics, optional. data – Kerword arguments of the data that is not in the statistics object, optional.

Here is an example on how to use the logger with a statistics object

>>> s = Statistics(n=2)
>>> s.register("mean", mean)
>>> s.register("max", max)
>>> s.update([1, 2, 3, 4], index=0)
>>> s.update([5, 6, 7, 8], index=1)
>>> l = EvolutionLogger(columns=["gen", "evals", "mean", "max"])
>>> l.logHeader()
gen      evals    mean     max
>>> l.logGeneration(gen="0_1", evals=4, stats=s, index=0)
0_1      4        [2.5000] [4.0000]
>>> l.logGeneration(gen="0_2", evals=4, stats=s, index=1)
0_2      4        [6.5000] [8.0000]

2.5. Checkpoint¶

class deap.tools.Checkpoint¶

A checkpoint is a file containing the state of any object that has been hooked. While initializing a checkpoint, add the objects that you want to be dumped by appending keyword arguments to the initializer or using the add().

In order to use efficiently this module, you must understand properly the assignment principles in Python. This module uses the pointers you passed to dump the object, for example the following won’t work as desired

>>> my_object = [1, 2, 3]
>>> cp = Checkpoint()
>>> cp.add("my_object", my_object)
>>> my_object = [3, 5, 6]
>>> cp.dump(open("example.ecp", "w"))
>>> cp.load(open("example.ecp", "r"))
>>> cp["my_object"]
[1, 2, 3]

In order to dump the new value of my_object it is needed to change its internal values directly and not touch the label, as in the following

>>> my_object = [1, 2, 3]
>>> cp = Checkpoint()
>>> cp.add("my_object", my_object)
>>> my_object[:] = [3, 5, 6]
>>> cp.dump(open("example.ecp", "w"))
>>> cp.load(open("example.ecp", "r"))
>>> cp["my_object"]
[3, 5, 6]

dump(filestream)¶

Dump the current registered object values in the provided filestream.

Parameters:	filestream – A stream in which write the data.

load(filestream)¶

Load a checkpoint from the provided filestream retrieving the dumped object values, it is not safe to load a checkpoint file in a checkpoint object that contains references as all conflicting names will be updated with the new values.

Parameters:	filestream – A stream from which to read a checkpoint.

add(name, object[, key])¶

Add an object to the list of objects to be dumped. The object is added under the name specified by the argument name, the object added is object, and the key argument allow to specify a subpart of the object that should be dumped (key defaults to an identity key that dumps the entire object).

Parameters:	name – The name under which the object will be dumped. object – The object to register for dumping. key – A function access the subcomponent of the object to dump, optional.

The following illustrates how to use the key.

>>> from operator import itemgetter
>>> my_object = [1, 2, 3]
>>> cp = Checkpoint()
>>> cp.add("item0", my_object, key=itemgetter(0))
>>> cp.dump(open("example.ecp", "w"))
>>> cp.load(open("example.ecp", "r"))
>>> cp["item0"]
1

remove(name[, ...])¶

Remove objects with the specified name from the list of objects to be dumped.

Parameters:	name – The name of one or more object to remove from dumping.

2.6. History¶

class deap.tools.History¶

The History class helps to build a genealogy of all the individuals produced in the evolution. It contains two attributes, the genealogy_tree that is a dictionary of lists indexed by individual, the list contain the indices of the parents. The second attribute genealogy_history contains every individual indexed by their individual number as in the genealogy tree.

The produced genealogy tree is compatible with NetworkX, here is how to plot the genealogy tree

history = History()

# Decorate the variation operators
toolbox.decorate("mate", history.decorator)
toolbox.decorate("mutate", history.decorator)

# Create the population and populate the history
population = toolbox.population(n=POPSIZE)
history.update(population)

# Do the evolution, the decorators will take care of updating the
# history
# [...]

import matplotlib.pyplot as plt
import networkx

graph = networkx.DiGraph(history.genealogy_tree)
graph = graph.reverse()     # Make the grah top-down
colors = [toolbox.evaluate(history.genealogy_history[i])[0] for i in graph]
networkx.draw(graph, node_color=colors)
plt.show()

Using NetworkX in combination with pygraphviz (dot layout) this amazing genealogy tree can be obtained from the OneMax example with a population size of 20 and 5 generations, where the color of the nodes indicate there fitness, blue is low and red is high.

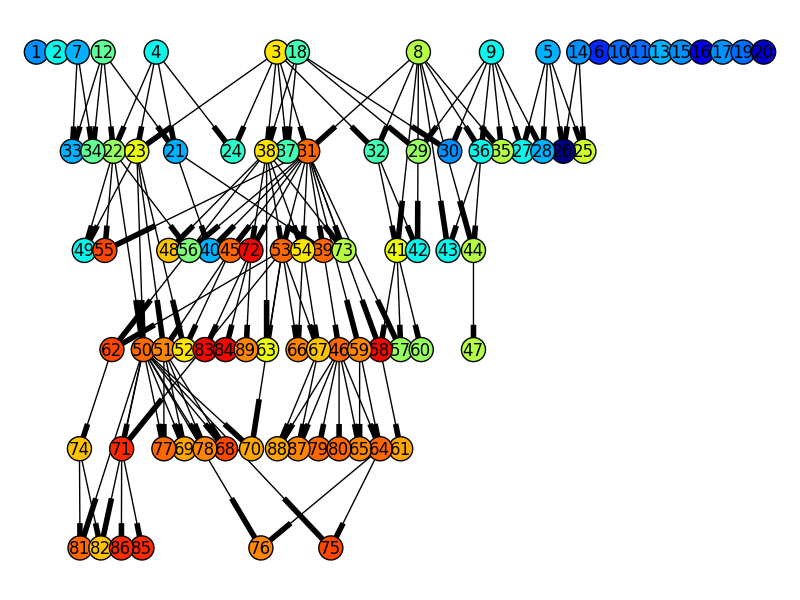
Note

The genealogy tree might get very big if your population and/or the number of generation is large.

update(individuals)¶

Update the history with the new individuals. The index present in their history_index attribute will be used to locate their parents, it is then modified to a unique one to keep track of those new individuals. This method should be called on the individuals after each variation.

Parameters:	individuals – The list of modified individuals that shall be inserted in the history.

If the individuals do not have a history_index attribute, the attribute is added and this individual is considered as having no parent. This method should be called with the initial population to initialize the history.

Modifying the internal genealogy_index of the history or the history_index of an individual may lead to unpredictable results and corruption of the history.

decorator¶: Property that returns an appropriate decorator to enhance the operators of the toolbox. The returned decorator assumes that the individuals are returned by the operator. First the decorator calls the underlying operation and then calls the update() function with what has been returned by the operator. Finally, it returns the individuals with their history parameters modified according to the update function.

getGenealogy(individual[, max_depth])¶

Provide the genealogy tree of an individual. The individual must have an attribute history_index as defined by update() in order to retrieve its associated genealogy tree. The returned graph contains the parents up to max_depth variations before this individual. If not provided the maximum depth is up to the begining of the evolution.

Parameters:	individual – The individual at the root of the genealogy tree. max_depth – The approximate maximum distance between the root (individual) and the leaves (parents), optional.
Returns:	A dictionary where each key is an individual index and the values are a tuple corresponding to the index of the parents.

2. Evolutionary Tools¶

2.1. Operators¶

2.1.1. Initialization¶

2.1.2. Crossover¶

2.1.3. Mutation¶

2.1.4. Selection¶

2.1.5. Bloat control¶

2.1.6. Migration¶

2.2. Statistics¶

2.3. Hall-Of-Fame¶

2.4. Evolution Logger¶

2.5. Checkpoint¶

2.6. History¶

Table Of Contents

Previous topic

Next topic

This Page

Navigation

2. Evolutionary Tools¶

2.1. Operators¶

2.1.1. Initialization¶

2.1.2. Crossover¶

2.1.3. Mutation¶

2.1.4. Selection¶

2.1.5. Bloat control¶

2.1.6. Migration¶

2.2. Statistics¶

2.3. Hall-Of-Fame¶

2.4. Evolution Logger¶

2.5. Checkpoint¶

2.6. History¶

Table Of Contents

Previous topic

Next topic

This Page

Quick search

Navigation